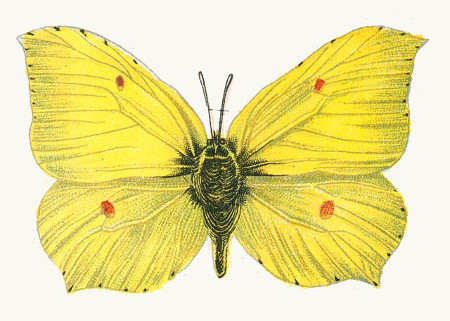
Just before his death in 1702, butterfly collector William Charlton delivered an unusual specimen to London entomologist James Petiver. Petiver wrote, “It exactly resembles our English Brimstone Butterfly (R. Rhamni), were it not for those black spots and apparent blue moons on the lower wings. This is the only one I have seen.” Carl Linnaeus named it Papilio ecclipsis and included it in the 12th edition of his Systema Naturae in 1767.
It wasn’t until 1793 that Danish zoologist Johan Christian Fabricius discovered that the dark patches had been painted on — it was only an ordinary brimstone butterfly after all. The curator at the British Museum “indignantly stamped the specimen to pieces” at this news, but entomologist William Jones created two new replicas to commemorate the “Charlton Brimstones.”