When the Seattle Art Museum presented an exhibition of Michelangelo’s early drawings in 2009, it included three menus that the sculptor had scrawled on the back of an envelope in 1518 — grocery lists for a servant.
Oregonian reviewer Steve Duin explained, “Because the servant he was sending to market was illiterate, Michelangelo illustrated the shopping lists — a herring, tortelli, two fennel soups, four anchovies and ‘a small quarter of a rough wine’ — with rushed (and all the more exquisite for it) caricatures in pen and ink.”
Related: In the 1490 manuscript below, Leonardo da Vinci tries to list successive doublings of 2 but mistakenly calculates 213 as 8092:
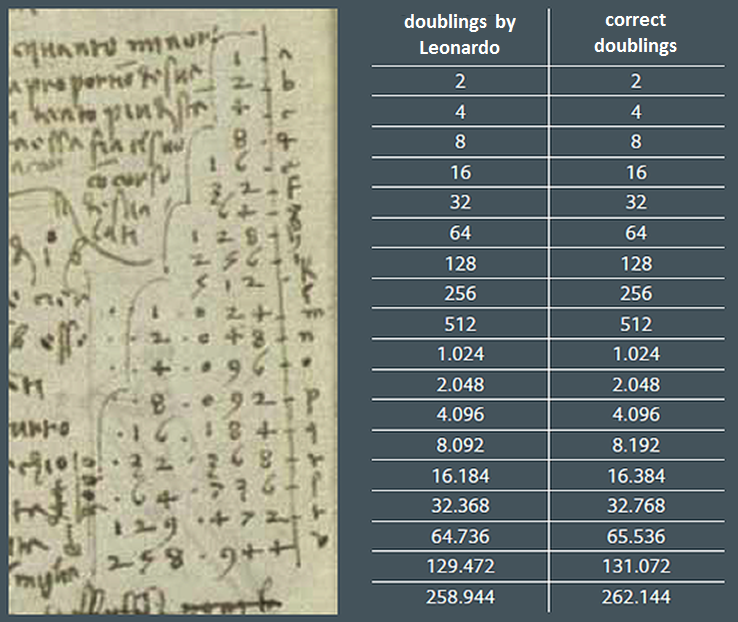
“Unmistakable this is a miscalculation of Leonardo and not of some sloppy copyists, as it was found in the original (mirrored) manuscript of da Vinci himself,” notes Ghent University computer scientist Peter Dawyndt. “That it was only discovered right now, five hundred years after da Vinci’s death, is probably due to the late discovery of the manuscript, barely fifty years ago.”
(Thanks, Peter.)