Beginning poker players are often shown a table like this:
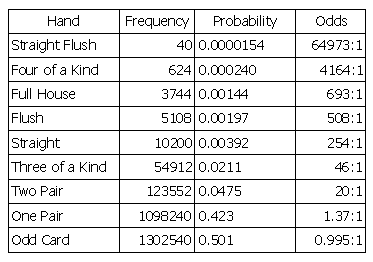
It’s straightforward enough, assigning a hierarchy to the hands based on the likelihood of their appearance. But a strange thing happens when wild cards are introduced. Suppose we add one wild joker:
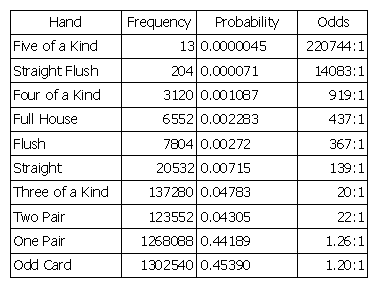
Now three of a kind is more likely (and thus less valuable) than two pair. Well, can we just reverse their places in the table? No, we can’t, because the wild card permits some players to reinterpret their hands. If you’re holding 6♠ 6♥ 7♣ 10♦ plus the joker, and we change the table, you’ll simply decide you’re holding two pair rather than three of a kind. So will everyone in your position. In fact, if we recalculate the odds with this expectation, we find that two pair has again become the more likely hand (13:1 vs. 34:1).
This can go on all day. Whenever a hand is declared “rare” it becomes popular — and thus not rare. The bottom line is that when wild cards are allowed, it becomes impossible to rank hands based on frequency.
From Julian Havil, Impossible?, 2008.