A puzzle by Soviet science writer Yakov Perelman: A bottle full of gasoline has a mass of 1,000 grams. The same bottle filled with acid has a mass of 1,600 grams. The acid is twice as dense as the gasoline. What’s the mass of the bottle?
The Peirce-Putnam Paradox
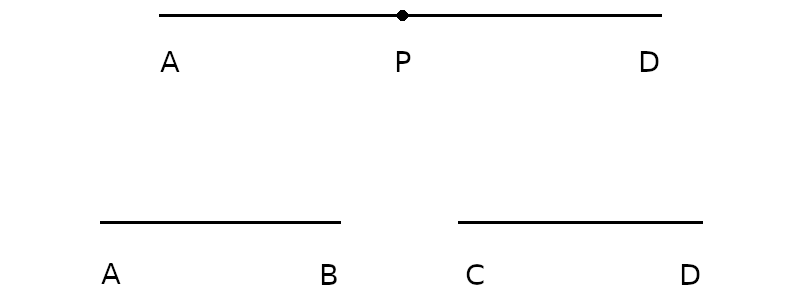
Divide line interval AD at point P and separate the halves by a short distance.
What’s happened to point P? Did it become point B or C? It seems wrong to say that it’s neither of these, or that it’s only one of them.
But if the single point P has “become” the two points B and C, how can we say it was a dimensionless object?
(Hilary Putnam, “Peirce’s Continuum,” in Kenneth Laine Ketner, ed., Peirce and Contemporary Thought: Philosophical Inquiries, 1995, via Piotr Łukowski, Paradoxes, 2011.)
Illumination

Allegedly this scheme was invented by a poet who wanted to write all night without interruption. He set up a row of candles and linked the base of each to the top of the next with a piece of twine. When the first candle burned down to the twine, “the latter naturally caught fire, and a tongue of flame would creep up to the adjoining candle, lighting it in the manner desired.”
“The scheme is a pretty example of the brilliancy of simplicity in idea, as compared with the complicated arrangements often devised to secure simple results.”
(James Scott, “Strange Devices,” Strand, August 1895, 184-189.)
Win Count
Imagine a game of tic-tac-toe (noughts and crosses) played in three dimensions in an 8×8×8 cube. A player wins by marking some straight line of eight cells through the large cube. How many such winning lines are there?
Keep Away

A notable adaptation: The forewing tips of the Atlas moth, Attacus atlas, resemble the heads of snakes.
When the moth encounters predators in its native Asian forests, the movement of its wings exaggerates the resemblance.
Insight

“Ideas often flash across our minds more complete than we could make them after much labor.” — La Rochefoucauld
“After investigating a problem in all directions, happy ideas come unexpectedly, without effort, like an inspiration. So far as I am concerned, they have never come to me when my mind was fatigued, or when I was at my working table. … They came particularly readily during the slow ascent of wooded hills on a sunny day.” — Hermann von Helmholtz
“You cannot, with your best deliberation and heed, come so close to any question as your spontaneous glance shall bring you while you rise from your bed or walk abroad in the morning after meditating the matter before sleep on the previous night.” — Emerson
“Three Threes Are Ten”
This little trick often puzzles many:–
Place three matches, coins, or other articles on the table, and by picking each one up and placing it back three times, counting each time to finish with number 10, instead of 9. Pick up the first match and return it to the table saying 1; the same with the second and third, saying 2 and 3; repeat this counting 4; but the fifth match must be held in the hand, saying at the time it is picked up, 5; the other two are also picked up and held in hand, making 6 and 7; the three matches are then returned to the table as 8, 9, and 10. If done quickly few are able to see through it.
— John Scott, The Puzzle King, 1899
04/20/2024 Reader Vladamir Tsepis adds, “This reminds me of the way to convince children you have 11 fingers. Start by showing your left hand splayed, curl down the thumb and index finger counting ‘one, two…’, then of the remaining say ‘let’s skip these three’. Move to your right hand, bend each finger in turn as you count ‘four, five, six, seven, eight…’. Return to the left hand counting off the three we skipped ‘nine, ten, eleven.'”
Fair and Square
From Lee Sallows:
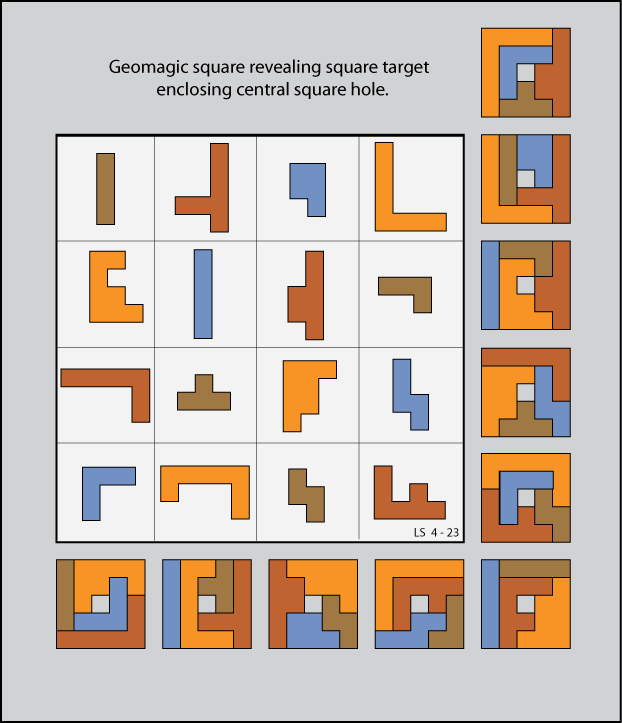
(Thanks, Lee!)
Memorial
From The Book of 500 Curious Puzzles, 1859:
Following is the epitaph of Ellinor Bachellor, an old pie woman. How should we read it?
Bene A. Thin Thed Ustt HEMO. Uld yo
L.D.C. RUSTO! Fnel L.B.
Ach El Lor. Lat. ELY,
Wa. S. shove N. W. How — Ass! kill’d I. N. T. H.
Ear T. Sofp, I, Escu Star.
D. San D T Art. San D K. N E. W. E
Ver — Yus E. — Oft He ove N, W. Hens He
‘Dli V’DL. on geno
Ug H S hem A.D.E. he R. la Stp. Uf — fap
Uf. F. B Y he. R hu
S. Ban D. M.
Uch pra is ‘D. No. Wheres Hedot
HL. i. e. Tom. A kead I.R.T.P. Yein hop Esthathe
R. C. RUSTWI,
L L B. Era is ‘–D!
The Stroke
When John Hollander claimed that English has no rhyme for bilge, George Starbuck imagined advancing on him, calling him a killjoy.
“No don’t!” Hollander cried. “I’m not a killj–“
