When Louis Philippe was deposed, why did he lose less than any of his subjects?
Because, while he lost only a crown, they lost a sovereign.
— Edith Bertha Ordway, The Handbook of Conundrums, 1915
“Extra Magic” Realized
From Lee Sallows:
The drawing at left above shows an unusual type of 3×3 geomagic square, being one in which the set of four pieces occupying each of the square’s nine 2×2 subsquares can be assembled so as to tile a 4×8 rectangle. The full set of subsquares become more apparent when it is understood that the square is to be viewed as if drawn on a torus, in which case its left-hand and right-hand edges will coincide, as will its upper and lower edges. In an earlier attempt at producing such a square several of the the pieces used were disjoint, or broken into separated fragments. Here, however, the pieces used are nine intact octominoes.
(Thanks, Lee!)
Going Home
Until 2006, a British ambassador leaving his post would write a valedictory despatch to be circulated among select readers in the British government. These “parting shots” tended to be appallingly frank, combining the diplomat’s real feelings about the nation he was leaving with his often wounded resentment at the indifference of his own government:
- Argentina: “All I knew of Argentines before coming here was that they were generally disliked by all other Latin Americans as unduly pretentious, snobbish upstarts. …. The per capita outlay on deodorants in the Argentine is the highest in the world.”
- Finland: “It could plausibly be argued that it is a misfortune for anybody but a Finn to spend three years in Finland, as I have just done. … Finland is flat, freezing, and far from the pulsating centres of European life.”
- Uruguay: “After living now for over two years among people who call themselves Orientals and who seem to have inherited nearly all the faults and none of the virtues of Spain (though they have many minor virtues of their own), I look forward to returning to what I conceive to be, at least by contrast, the speed and efficiency of my own country.”
- Saudi Arabia: “It is a great tragedy that, with all the world’s needs, Providence should have concentrated so much of a vital resource and so much wealth in the hands of people who need it so little and are so socially irresponsible about the use of it.”
- Thailand: “Decayed garbage left for months on the side of the roads; stagnant canals that serve both as cesspools and as the dumping ground for dead dogs; buses and lorries that belch uncontrolled clouds of diesel fumes; scarcely a pavement without potholes and open manholes to break the legs of the unwary; bag-snatchers in every block; assault and violence a way of life; prostitution and every form of natural and unnatural vice on a scale astonishing even in Asia; a city of 4 million with only one park, and that littered with refuse and infested by thieves; unplanned hideous ribbon development; no proper drainage, so that in the rainy season large areas of the city remain flooded for weeks on end; and the whole set in a flat mournful plain without even a hillock in sight for 100 miles in any direction: this is Bangkok, the vaunted Venice of the East.”
Matthew Parris, who published a whole collection of these in 2010, explains: “Beyond retirement there can be no reprisals.”
The Bottom Line
In his 2008 book 100 Essential Things You Didn’t Know You Didn’t Know, cosmologist John D. Barrow considers how long a straight line a typical HB pencil could draw before the lead was exhausted.
A soft 2B pencil draws a line about 20 nanometers thick, and the diameter of a carbon atom is 0.14 nanometers, so a pencil line is only about 143 atoms thick. The pencil lead has a radius of about a millimeter, so its area is about π square millimeters. If the pencil is 15 centimeters long, then it contains 150π cubic millimeters of graphite.
Putting this together, if we draw a line 20 nanometers thick and 2 millimeters wide, then the pencil contains enough graphite to continue for the surprising distance L = 150π / 4 × 10-7 millimeters = 1,178 kilometers. “But I haven’t tested this prediction!”
(Thanks, Larry.)
05/21/2022 RELATED: How much of a pencil’s lead is wasted in the sharpening?
(Thanks, Chris.)
Birds of a Feather
A problem from the February 2006 issue of Crux Mathematicorum:
Prove that if 10a + b is a multiple of 7 then a – 2b must be a multiple of 7 as well.
Napkin Proof
A sure-fire way to avoid hangover, from philosopher Josh Parsons:
It’s well known that one can alleviate hangover symptoms with a “hair of the dog” — another alcoholic drink. The problem is that this incurs another later hangover.
But think about this. Suppose that a pint of beer produces an hour of drunkenness followed by an hour of hangover, and that smaller quantities produce proportionately shorter periods. Begin, then, from a sober state, and drink half a pint of beer. Wait half an hour, until you’re just about to start feeling the hangover. Then drink a quarter pint of beer and wait a quarter of an hour, then an eighth of a pint, and so on. After an hour, you will have drunk one pint of beer and experienced no hangover, as it’s manifestly true that every incipient hangover you had was prevented by a further drink.
In his paper, cited below, Parsons addresses some objections to this scheme, including the fact that most publicans won’t stock 1/64-pint glasses and that eventually you’ll be swallowing at greater than light speed, and indeed swallowing something that may no longer qualify as beer. He grants that the task might be a “medical impossibility.”
But “by the time you get to the point where you can’t continue, you will only be incurring a very very short hangover with your last sip of beer. You don’t mind suffering a millisecond’s hangover. Besides, isn’t it worth speculating about whether the cure would work, on the counterfactual supposition that you can swallow at any finite speed, and that alcoholic beverages are made out of infinitely divisible gunk? Such speculations can tell us a lot about our concepts of infinity and matter.”
(He thanks “my colleagues and students for many helpful suggestions, and Central Bar for providing a pleasant environment in which to test my theories.”)
(Josh Parsons, “The Eleatic Hangover Cure,” Analysis 64:4 [October 2004], 364-366.)
Two-Step
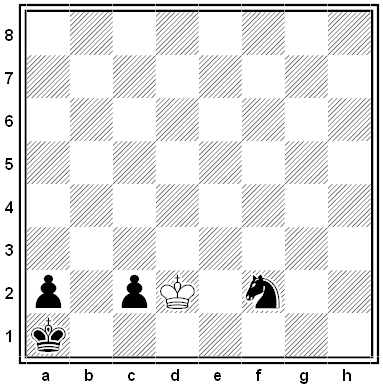
In this position, devised by Harvard mathematician Noam Elkies, White is in serious trouble. He’s been reduced to a bare king, and his opponent has a knight as well as two pawns on the verge of queening.
It’s tempting to snap up the c2 pawn — this gains material and keeps Black’s king bottled up in the corner, which stops the a-pawn from queening. But now Black can win with 1. … Nd3! This stops the white king from moving to c1, which had been his only way to keep the black king immobilized. Now he’ll have to back off (even though perhaps winning the knight), and Black will play 2. … Kb1 and queen his pawn.
Interestingly, in the original position if White plays 1. Kc1, he’s guaranteed a draw: He can capture the c2 pawn on his next move and then shuffle happily forever between c1 and c2. Because he’s “lost a move,” Black can’t execute the maneuver described above to force the white king away from the corner. That’s because as the white king shuffles between a white and a black square, the knight must move about the board, also alternating between squares of different colors — and always landing on the wrong color to achieve his goal. The knight can wander as far afield as he likes, and execute any complex maneuver; he’ll always arrive at the wrong moment to achieve his aim.
(Noam D. Elkies and Richard P. Stanley, “The Mathematical Knight,” Mathematical Intelligencer 25:1 [December 2003], 22-34.)
“The Pavior”
An Author saw a Laborer hammering stones into the pavement of a street, and approaching him said:
‘My friend, you seem weary. Ambition is a hard taskmaster.’
‘I’m working for Mr. Jones, sir,’ the Laborer replied.
‘Well, cheer up,’ the Author resumed; ‘fame comes at the most unexpected times. To-day you are poor, obscure and disheartened, but to-morrow the world may be ringing with your name.’
‘What are you telling me?’ the Laborer said. ‘Can not an honest pavior perform his work in peace, and get his money for it, and his living by it, without others talking rot about ambition and hopes of fame?’
‘Can not an honest writer?’ said the Author.
— Ambrose Bierce, The Monk and the Hangman’s Daughter, 1911
The Bar Problem
Suppose a local bar has 100 regular patrons. The bar is rather small, and going there is enjoyable on a given night only if fewer than 60 people show up. This is a problem: I want to go to the bar, but I expect to enjoy it only if you don’t come. But I know that you’re thinking the same thing about me. If no one communicates in advance, how many people will tend to turn up at the bar?
In a 1994 computer experiment, Stanford University economist W. Brian Arthur assigned each patron a set of plausible predictive rules on which it might base its decision. One rule might predict that next week’s attendance will be the same as last week’s, while another might take a rounded average of the last four weeks, and so on. Then, in practice, each patron would downgrade its badly performing rules and promote the more successful ones, and revise these ratings continually.
What he found is that the mean attendance converges to about 60, forming an “emergent ecology” that Arthur said is “almost organic in nature.” The population of active predictors splits into a 60/40 ratio, even though it keeps changing in membership forever. “To get some understanding of how this happens, suppose that 70 percent of their predictors forecasted above 60 for a longish time. Then on average only 30 people would show up; but this would validate predictors that forecasted close to 30 and invalidate the above-60 predictors, restoring the ‘ecological’ balance among predictions, so to speak.”
This is heartening to see, because life is full of such murky decisions. “There is no deductively rational solution — no ‘correct’ expectational model,” Arthur writes. “From the agents’ viewpoint, the problem is ill-defined, and they are propelled into a world of induction.”
(W. Brian Arthur, “Inductive Reasoning and Bounded Rationality,” American Economic Review 84:2 [May 1994], 406-411.)
Unquote
“Foreign nations are a contemporaneous posterity.”
— “A forgotten American essayist,” quoted by Brander Matthews in his introduction to The Oxford Book of American Essays, 1914