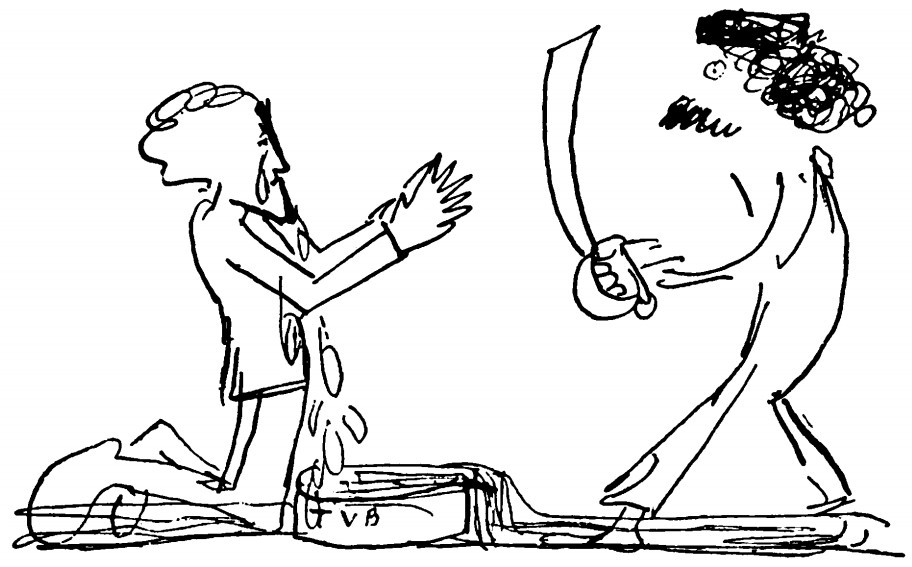
I just liked this: When Augustus Saint-Gaudens broke an engagement with Mark Twain, he sent him this wordless apology.
(From Albert Bigelow Paine’s 1912 biography of Twain.)

I just liked this: When Augustus Saint-Gaudens broke an engagement with Mark Twain, he sent him this wordless apology.
(From Albert Bigelow Paine’s 1912 biography of Twain.)
In a 1978 article in the New England Journal of Medicine, Massachusetts General Hospital psychiatrist James E. Groves categorized the patients “whom most physicians dread”:
“Dependent clingers” escalate from normal requests for reassurance to “repeated, perfervid, incarcerating cries for explanation, affection, analgesics, sedatives and all forms of attention imaginable.” They may have severe, even life-threatening disorders, or they may have no discernible illness at all.
“Entitled demanders” use “intimidation, devaluation and guilt-induction to place the doctor in the role of the inexhaustible supply depot.” They may even try to control the doctor by withholding payment or threatening to sue.
“Manipulative help-rejecters” appear almost smugly satisfied, returning “again and again to the office or clinic to report that, once again, the regimen did not work.” When one symptom is relieved, another appears in its place.
“Self-destructive deniers” show “unconsciously self-murderous behaviors, such as the continued drinking of a patient with esophageal varices and hepatic failure.” These patients “seem to glory in their own destruction. They appear to find their main pleasure in furiously defeating the physician’s attempts to preserve their lives.”
“Admitted or not, the fact remains that a few patients kindle aversion, fear, despair or even downright malice in their doctors,” Groves wrote, noting that the medical literature had largely failed to address this problem. “Emotional reactions to patients cannot simply be wished away, nor is it good medicine to pretend that they do not exist.”
(James E. Groves, “Taking Care of the Hateful Patient,” New England Journal of Medicine, April 20, 1978.)
A Slander traveling rapidly through the land upon his joyous mission was accosted by a Retraction and commanded to halt and be killed.
‘Your career of mischief is at an end,’ said the Retraction, drawing his club, rolling up his sleeves and spitting on his hands.
‘Why should you slay me?’ protested the Slander. ‘Whatever my intentions were, I have been innocuous, for you have dogged my strides and counteracted my influence.’
‘Dogged your grandmother!’ said the Retraction, with contemptuous vulgarity of speech. ‘In the order of nature it is appointed that we two shall never travel the same road.’
‘How then,’ the Slander asked, triumphantly, ‘have you overtaken me?’
‘I have not,’ replied the Retraction; ‘we have accidentally met. I came round the world the other way.’
But when he tried to execute his fell purpose he found that in the order of nature it was appointed that he himself perish miserably in the encounter.
— Ambrose Bierce, Fantastic Fables, 1899
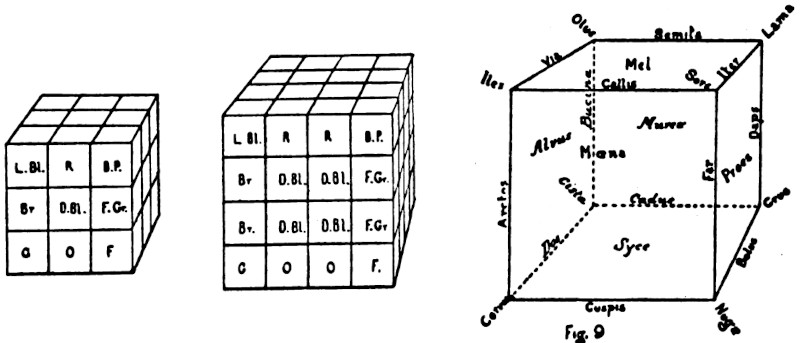
In 1880 Charles Hinton (inventor of the baseball gun) turned his attention to the fourth dimension, that unseen world whose behavior seems so baffling to ordinary thinkers.
In his 1888 book A New Era of Thought, he announced a unique way to think about it, a set of 81 colored cubes that correspond to the 81 parts of a 3 × 3 × 3 × 3 hypercube. By creating a set of wooden cubes, painting them according to Hinton’s instructions, and working through the prescribed exercises, the reader could learn to visualize the fourth dimension as intuitively as the third:
The square, in moving in the unknown direction, traces out a succession of squares, the assemblage of which makes the cube in layers. So also the cube, moving in the unknown direction, will at any point of its motion, still be a cube; and the assemblage of cubes thus placed constitutes the tessaract in layers. We suppose the cube to change its colour directly it begins to move. Its colour between 1 and 2 we can easily determine by finding what colours its different parts assume, as they move in the unknown direction.
Hinton’s method drew few adherents, but he was sure that it worked — he had proved it for himself. “The particular problem,” he wrote, “at which I have worked for more than ten years, has been completely solved. It is possible for the mind to acquire a conception of higher space as adequate as that of our three-dimensional space, and to use it in the same manner.”
He moved on to other things, but he’s left us one permanent calling card — Hinton coined the word tesseract.
A puzzle by Henry Dudeney:
When visiting with a friend one of our hospitals for wounded soldiers, I was informed that exactly two-thirds of the men had lost an eye, three-fourths had lost an arm, and four-fifths had lost a leg. ‘Then,’ I remarked to my friend, ‘it follows that at least twenty-six of the men must have lost all three — an eye, an arm, and a leg.’ That being so, can you say exactly how many men were in the hospital? It is a very simple calculation, but I have no doubt it will perplex a good many readers.

Here’s a striking sign of the pervasive influence of the Industrial Revolution: It darkened England’s moths. Before 1811, the peppered moth, Biston betularia, had a white body. But as soot darkened trees, lighter-bodied insects became more visible to birds and other predators. By 1848 the frequency of dark-bodied moths in industrial regions had increased dramatically, one of the first documented instances of Darwin’s principle of natural selection. American geneticist Sewall Wright called it “the clearest case in which a conspicuous evolutionary process has actually been observed.”
Somewhat related: A curious wartime observation by Gertrude Stein, in Alsace, from The Autobiography of Alice B. Toklas:
Another thing that interested us enormously was how different the camouflage of the french looked from the camouflage of the germans, and then once we came across some very neat camouflage and it was american. The idea was the same but as after all it was different nationalities who did it the difference was inevitable. The colour schemes were different, the designs were different, the way of placing them was different, it made plain the whole theory of art and its inevitability.
“Perchance the best chance of reproducing the ancient Greek temperament would be to cross the Scots with the Chinese.” — Hugh McDiarmid
In 1837 English journalist Albany Fonblanque wrote, “Sir Robert Peel was a smooth round peg, in a sharp-cornered square hole, and Lord Lyndenurst is a rectangular square-cut peg, in a smooth round hole.”
Which of these is the better fit? In other words, which is larger, the ratio of the area of a circle to a circumscribed square, or the area of a square to a circumscribed circle?
In two dimensions, these ratios work out to π/4 and 2/π, respectively, so a round peg fits better into a square hole than a square peg into a round hole.
But, strangely, Berkeley mathematician David Singmaster discovered in 1964 that this is true only in dimensions less than 9. For n ≥ 9 the n-dimensional unit cube fits more closely into the n-dimensional unit sphere than vice versa.
There’s a moral in there, but I don’t know what it is.
(David Singmaster, “On Round Pegs in Square Holes and Square Pegs in Round Holes,” Mathematics Magazine 37:5 [November 1964], 335-337.)

The wordplay journal Word Ways has made a tradition of revising the familiar rhyme “Mary Had a Little Lamb” under various constraints. Some examples:
Alliteration: James Puder, WW February 1998
Astral Aries’ avatar, alabaster “Aly,”
Ann adopted; allies are Ann and Ann’s argali.
Ann, an able autodidact, academic angst avoids;
And arch Aly’s Argus-eyed act awes astonished anthropoids.
Pangram (uses all 26 letters): A. Ross Eckler, WW February 1989
Mary had a little lamb with fleece extremely white;
Instead of grazing, all alone, the lamb kept her in sight.
It followed her to school one day, which was against the rule;
The children thought it quite a joke to view a lamb in school.
Words formed of chemical element symbols: WW February 2008
ONe TiNY AgNUS SHe NoW OWNS (SNOW-WHITe IS HEr CoAt),
WHeN HEr LaDy IS NeArBY, AgNUS STaYS, I NoTe.
In ClAsS ONe MoRn SHe TaKEs HEr PLaCe; TeAcHEr CrIEs “SHoO! RUN!”
HeAr THoSe LaSSiEs ScReAm “HoW CuTe!” ThIS AgNUS — PURe FUN!”
Four-letter words: Dave Morice, WW November 2006
Mary kept some tiny lamb with wool hued just like snow,
Each spot that this girl, Mary, went, that lamb went also (slow).
Once lamb went past home room with girl. That bent some rule last year.
This made kids loud, glad, made them play: they eyed lamb very near.
Three-letter and shorter words: Jeff Grant, WW May 2004
Amy had an ewe so wee, it was an icy hue,
And any way our Amy led, the ewe it did go too.
It ran in to her den one day (an act not in the law).
Oh, the fun for boy and gal! The ewe so wee all saw.

Nominative determinism is the theory that people gravitate toward occupations that reflect their names. In 1994 New Scientist noted that a new book, Pole Positions: The Polar Regions and the Future of the Planet, had been written by one Daniel Snowman, and that another, London Under London: A Subterranean Guide, received just two weeks later, had been written by Richard Trench. Psychologist Jen Hunt of the University of Manchester pointed out an article on incontinence in the British Journal of Urology whose authors were A.J. Splatt and D. Weedon.
If the theory is valid, then the naming of children is more momentous than we think. Harry Truman’s vice president, Alben William Barkley, above, was originally named Willie Alben Barkley, and contended that no one named Willie Alben could be elected superintendent of the county poorhouse. He changed his name to Alben William.
“In fact,” he wrote in his autobiography, “I think one of the graver shortcomings of my long career as a lawmaker was my failure to introduce a bill making it mandatory for parents to postpone the naming of their children until the youngsters are old enough to pick out a name for themselves.”