Mission Accomplished

The Royal Mail just delivered this letter, correctly, to Catrina Davies of Cornwall, who had discussed affordable housing on travel documentarian Simon Reeve’s BBC series in November.
“It’s just great that they made the effort and didn’t just throw it away,” Davies said.
On the envelope, the sender had written, “Royal Mail never fails.”
(Thanks, Alex.)
Inventory
The following pair of sentences employ 2 ‘0’s, 2 ‘1’s, 9 ‘2’s, 5 ‘3’s, 5 ‘4’s, 4 ‘5’s, 5 ‘6’s, 2 ‘7’s, 3 ‘8’s and 3 ‘9’s.
The sentences above and below employ 2 ‘0’s, 2 ‘1’s, 8 ‘2’s, 6 ‘3’s, 5 ‘4’s, 6 ‘5’s, 3 ‘6’s, 2 ‘7’s, 2 ‘8’s and 4 ‘9’s.
The previous pair of sentences employ 2 ‘0’s, 2 ‘1’s, 9 ‘2’s, 5 ‘3’s, 4 ‘4’s, 6 ‘5’s, 4 ‘6’s, 2 ‘7’s, 3 ‘8’s and 3 ‘9’s.
(From Lee Sallows and Victor L. Eijkhout, “Co-Descriptive Strings,” Mathematical Gazette 70:451 [March 1986], 1-10.)
The British Flag Theorem
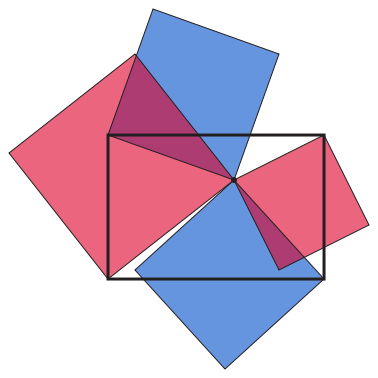
Draw a rectangle and pick a point inside it. Now the sum of the squares of the distances from that point to two opposite corners of the rectangle equals the sum to the other two opposite corners.
Above, the red squares have the same total area as the blue ones.
The Garden of Eden

When a building was razed in 1973 on Eldridge Street on Manhattan’s Lower East Side, local resident Adam Purple cleared the lot, gathered manure left by horse-drawn carriages around Central Park, and designed a garden laid out in concentric circles around a central yin-yang symbol. As nearby buildings were torn down he added further circles, until the garden filled 15,000 square feet with corn, cucumbers, cherry tomatoes, asparagus, black raspberries, and strawberries.
The city bulldozed Purple’s lot in 1986, but Richard Reynolds’ London-based blog now documents similar “guerrilla gardening” initiatives around the world.
Harmony
A problem from the January 1990 issue of Quantum: Forty-one rooks are placed on a 10 × 10 chessboard. Prove that some five of them don’t attack one another. (Two rooks attack one another if they occupy the same row or column.)
Do It Yourself
https://www.youtube.com/watch?v=x8zFL-0rBAw
Muhammad Didit’s accurately titled video “2 Hours Doing Nothing” has surpassed 5 million views on YouTube.
The (inevitable) mobile game has now been downloaded more than 10,000 times.
Quickie
One other quick item from Eureka, the journal of the Cambridge University Mathematical Society:
In its 1947 problem drive, the society proposed the following problem:
To find unequal positive integers x, y, z such that
x3 + y3 = z4.
“Although there were some research students in Theory of Numbers among those who tried, not one person succeeded in solving it within the time, yet the solution is extremely simple.” What is it?
Podcast Episode 348: Who Killed the Red Baron?

In 1918, German flying ace Manfred von Richthofen chased an inexperienced Canadian pilot out of a dogfight and up the Somme valley. It would be the last chase of his life. In this week’s episode of the Futility Closet podcast we’ll describe the last moments of the Red Baron and the enduring controversy over who ended his career.
We’ll also consider some unwanted name changes and puzzle over an embarrassing Oscar speech.
A Plate of 1,000 Cookies

A puzzle by David B., a mathematician at the National Security Agency, from the agency’s May 2017 Puzzle Periodical:
Steve, Tony, and Bruce have a plate of 1,000 cookies to share. They decide to share them in the following way: beginning with Steve, each of them in turn takes as many cookies as he likes (they must take an integer amount, greater than or equal to 1), and then passes the plate clockwise (with Tony sitting to Steve’s left, and Bruce sitting to Tony’s left). Nobody wants to feel like he hogged too many cookies, so they all want to avoid being the player at the end who has taken the most cookies. Additionally, nobody wants to feel cheated by finishing with the fewest cookies. Finally, given that the previous two conditions are definitely met, or definitely cannot be met, each player would like to maximize the number of cookies he eats. The players’ objectives can be summarized as follows:
Objectives:
- Have one player who has eaten more cookies than you, and one player who has eaten fewer cookies than you.
- Eat as many cookies as possible.
Objective #1 takes infinite priority over Objective #2. Assuming that all players are perfectly rational, that they are all aware of each other’s rationality and objectives, and that they cannot communicate with each other in any way, how many cookies should Steve take to ensure he meets both objectives and how many cookies will Tony and Bruce take if Steve takes the winning amount?