More Magic

Albrecht Dürer’s 1514 engraving Melencolia I includes this famous magic square: The magic sum of 34 can be reached by adding the numbers in any row, column, diagonal, or quadrant; the four center squares; the four corner squares; the four numbers clockwise from the corners; or the four counterclockwise.
In Power Play (1997), University of Toronto mathematician Ed Barbeau points out that there’s even more magic when we consider squares and cubes. Take the numbers in the first two and the last two rows:
16 + 3 + 2 + 13 + 5 + 10 + 11 + 8 = 9 + 6 + 7 + 12 + 4 + 15 + 14 + 1
162 + 32 + 22 + 132 + 52 + 102 + 112 + 82 = 92 + 62 + 72 + 122 + 42 + 152 + 142 + 12
Or alternate columns:
16 + 5 + 9 + 4 + 2 + 11 + 7 + 14 = 3 + 10 + 6 + 15 + 13 + 8 + 12 + 1
162 + 52 + 92 + 42 + 22 + 112 + 72 + 142 = 32 + 102 + 62 + 152 + 132 + 82 + 122 + 12
Most amazingly, if you compare the numbers on and off the diagonals, this works with both squares and cubes:
16 + 10 + 7 + 1 + 13 + 11 + 6 + 4 = 2 + 3 + 5 + 8 + 9 + 12 + 14 + 15
162 + 102 + 72 + 12 + 132 + 112 + 62 + 42 = 22 + 32 + 52 + 82 + 92 + 122 + 142 + 152
163 + 103 + 73 + 13 + 133 + 113 + 63 + 43 = 23 + 33 + 53 + 83 + 93 + 123 + 143 + 153
Unknowns
In his 2014 book Describing Gods, Graham Oppy presents the “divine liar” paradox, by SUNY philosopher Patrick Grim:
1. X believes that (1) is not true.
If we suppose that (1) is true, then this tells us that X believes that (1) is not true. But if an omniscient being believes that (1) is not true, then it follows that (1) is not true. So the assumption that (1) is true leads to a contradiction.
Suppose instead that (1) is not true. That is, suppose that it’s not the case that X believes that (1) is not true. If an omniscient being fails to believe that (1) is not true, then it’s not true that (1) is not true. So this alternative also leads to a contradiction.
But, on the assumption that there is an omniscient being X, either it’s the case that (1) is true or it’s the case that (1) is not true.
“So, on pain of contradiction,” Oppy explains, “we seem driven to the conclusion that there is no omniscient being X.”
(Also: Patrick Grim, “Some Neglected Problems of Omniscience,” American Philosophical Quarterly 20:3 [July 1983], 265-276.)
Say It With Flowers

The lost art of floriography assigned meanings to flowers so that lovers could exchange messages with “talking bouquets.” In his 1839 Language of Flowers, English journalist Frederic Shoberl rendered an entire verse by French poet Évariste de Parny as the combination of 16 flowers:
Aimer est un destin charmant,
C’est un bonheur qui nous enivre,
Et qui produit l’enchantement.
Avoir aimé, c’est ne plus vivre,
Hélas! c’est avoir acheté
Cette accablante vérité,
Que les serments sont un mensonge,
Que l’amour trompe tôt ou tard,
Que l’innocence n’est qu’un art,
Et que le bonheur n’est qu’un songe.
“It may be thus rendered: ‘To love is a pleasure, a happiness, which intoxicates; to love no longer, is to live no longer; it is to have bought this sad truth, that innocence is falsehood, that love is an art, and that happiness is a dream.'”
Pillow Verse

English textile designer William Morris always said he wanted to dream a poem. When he finally did and was asked whether he could remember it, he said, “Only the first line, and it went like this: The moonlight slept on a treacle sea.”
Archbishop Edward Benson told Edmund Gosse that he dreamed he had been appointed poet laureate and found himself reciting this couplet to the queen:
Your latest atmosphere device
Is all composed of dust and lice.
And Sir John Squire confessed that when he dreamed the following lines they seemed impressive until he woke up:
There was a boy grew twenty inch, yes,
Twenty inch a year,
It might have made his mother flinch, but
She was quite a dear;
Yes, she was excellent,
And she was well content
To watch her offspring forge ahead in his
Peculiar sphere.
(From Stephen Brook, ed., The Oxford Book of Dreams, 1983. See Night Work.)
Line Work
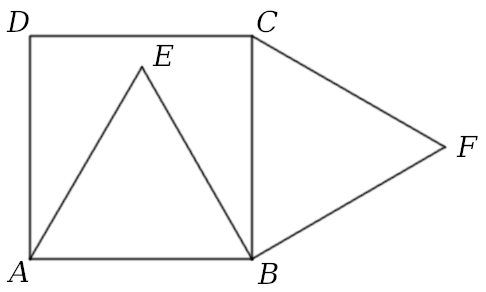
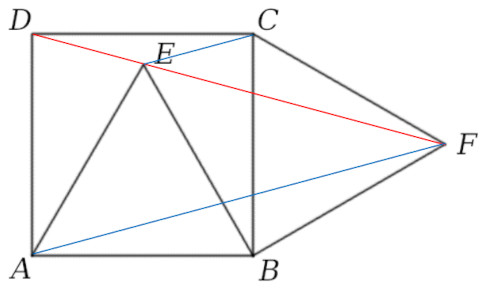
Robert Bilinski proposed this problem in the April 2006 issue of Crux Mathematicorum. On square ABCD, two equilateral triangles are constructed, ABE internally and BCF externally, as shown. Prove that D, E, and F are collinear.
Unquote

“It was the irony. It was the same irony that caused me to think, pause, and just inwardly chuckle, just momentarily, that, God, here are two guys further away from home … than two guys had ever been, but there are more people watching us than anybody else has ever watched two people before in history.” — Buzz Aldrin
Evolution Without Life
Philosopher Mark Bedau points out that, even on a dead planet, the microscopic crystallites that make up clay and mud seem to have the flexibility to adapt and evolve by natural selection:
- Crystals reproduce in the sense that when they become large enough they cleave and pieces break off, becoming seeds for new crystals. A population of reproducing crystals can become the setting for crystal “evolution.”
- All crystals have flaws, which are reproduced randomly and can become a source of novel information that gets expressed in “phenotypic” traits such as shape, growth rate, and the conditions that cause cleaving.
- Each new layer of crystals copies the geometrical arrangement of atoms in the layer below, and defects can be copied in the same way. Grain boundaries and dislocations in one crystal tend to be copied to its “offspring” and subsequent generations. Over time these “mutations” can produce “species” among which nature selects.
- A crystal’s shape, growth rate, and cleaving conditions all affect the rate at which it proliferates, and crystals with different properties will disperse and diffuse differently, which affects the rate at which they reproduce.
So a population of crystals can exhibit reproduction, variation, heredity, and adaptivity. “What is rather surprising is that, in the process, the planet remains entirely devoid of life. Thus, natural selection can take place in an entirely inorganic setting.”
(Mark Bedau, “Can Biological Teleology Be Naturalized?” Journal of Philosophy 88:11 [November 1991], 647-655. I think A.G. Cairns-Smith originated this idea in Seven Clues to the Origin of Life in 1985, and Richard Dawkins took it up in The Blind Watchmaker the following year.)
Moving Up
In the 1930s New York tackled its congestion problem by parking cars in the sky — for 50 cents an attendant would drive your car onto a hydraulic elevator and hoist it as much as 24 stories above street level, where it remained until you returned to claim it.
One “hotel for autos” had space to park a thousand cars, but it was soon obsolete — cars grew too big to fit in the stalls, and underground parking proved to be a cheaper solution. Kent Automatic Garages folded barely three years after it started, and the sites of its marvels are just anonymous office buildings.
(Thanks, Ron.)
03/26/2022 UPDATE: Hydraulic lifts are still being used! (Thanks, Jim.)
“Busy as a Fiddler’s Elbow”
Vivid comparisons, from Elyse Sommer and Mike Sommer’s Similes Dictionary, 1988:
- Love is like the moon; when it does not increase it decreases. (Joseph Alexandre Pierre Segur)
- Cities, like cats, will reveal themselves at night. (Rupert Brooke)
- Calm as a virgin discussing flower arrangement. (George MacDonald Fraser)
- The conversations … behaved like green logs, they fumed but would not fire. (Truman Capote)
- Fierce as a lobster making one last lunge out of the pot. (Norman Mailer)
- Dogged as a turtle crossing a road. (Marge Piercy)
- Confident as a man dialing his own telephone number. (Jack Bell)
- His mouth felt as if it had been to a party without him. (Peter De Vries)
- False economy is like stopping one hole in a sieve. (Samuel Johnson)
- Writers, like teeth, are divided into incisors and grinders. (Walter Bagehot)
“Strong men are made by opposition,” wrote Frank Harris. “Like kites they go up against the wind.”