Thus I
Passe by,
And die:
As One,
Unknown,
And gon:
I’m made
A shade,
And laid
I’th grave,
There have
My Cave.
Where tell
I dwell,
Farewell.
— Robert Herrick, “Upon His Departure Hence,” 1648
Thus I
Passe by,
And die:
As One,
Unknown,
And gon:
I’m made
A shade,
And laid
I’th grave,
There have
My Cave.
Where tell
I dwell,
Farewell.
— Robert Herrick, “Upon His Departure Hence,” 1648
Two ridiculous problems from Arthur Ford Mackenzie’s 1887 book Chess: Its Poetry and Its Prose:
Left: “White to mate without making a move.”
Right: “White to mate in 1/4 of a move.”
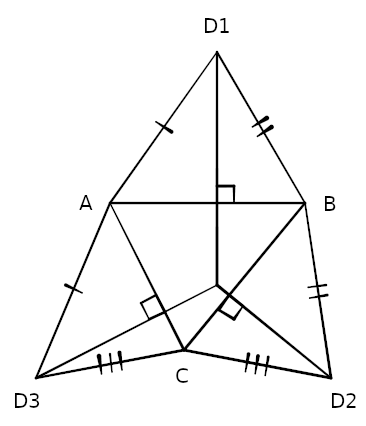
Consider a triangle ABC and three other triangles (ABD1, BCD2, and ACD3) that share common sides with it, and assume that the sides adjacent to any vertex of ABC are equal, as shown. The altitudes of the three outer triangles, passing through D1, D2, and D3 and orthogonal to the sides of ABC, meet in a point.
This can be made intuitive by imagining the figure in three dimensions. Fold each of the outer triangles “up,” out of the page. Their outer vertices will meet at the apex of a tetrahedron. Now if we imagine looking straight down at that apex and folding the sides down again, each of those vertices will follow the line of an altitude (from our perspective) on the way back to its original position, because each follows an arc that’s orthogonal to the horizontal plane and to one of the sides of ABC. The result is the original figure.
(Alexander Shen, “Three-Dimensional Solutions for Two-Dimensional Problems,” Mathematical Intelligencer 19:3 [June 1997], 44-47.)
The symptoms of a typical attack
A clearly ordered sequence seldom lack;
The first complaint is epigastric pain
Then vomiting will follow in its train,
After a while the first sharp pain recedes
And in its place right iliac pain succeeds,
With local tenderness which thus supplies
The evidence of where the trouble lies.
Then only — and to this I pray be wise —
Then only will the temperature rise,
And as a rule the fever is but slight,
Hundred and one or some such moderate height.
‘Tis only then you get leucocytosis
Which if you like will clinch the diagnosis,
Though in my own experience I confess
I find this necessary less and less.
From Zachary Cope, The Diagnosis of the Acute Abdomen in Rhyme, 1947.
Further to my March post “A Lucrative Loop,” reader Snehal Shekatkar of S.P. Pune University notes a similar discovery of iterates leading to strange cycles among natural numbers.
Here is a simple example. Take a natural number and factorize it (12 = 2 * 2 * 3), then add all the prime factors (2 + 2 + 3 = 7). If the answer is prime, add 1 and then factorize again (7 + 1 = 8 = 2 * 2 * 2) and repeat (2 + 2 + 2 = 6). Eventually ALL the natural numbers greater than 4 eventually get trapped in cycle (5 -> 6 -> 5). Instead of adding 1 after hitting a prime, if you add some other natural number A, then depending upon A, numbers may get trapped in a different cycle. For example, for A = 19, they eventually get trapped in cycle (5 -> 24 -> 9 -> 6 -> 5).
For some values of A, several cycles exist. For example, when A = 3, some numbers get trapped in cycle (5 -> 8 -> 6 -> 5) while others get trapped in the cycle (7 -> 10 -> 7).
(Made with Tian An Wong of Michigan University.) (Thanks, Snehal.)
A logic problem from Lewis Carroll: What conclusion follows from these premises?
Gods chase
Round vase.
What say?
What play?
Don’t know.
Nice, though.
— Desmond Skirrow

In the 1890s, Waldemar Haffkine worked valiantly to develop vaccines against both cholera and bubonic plague. Then an unjust accusation derailed his career. In this week’s episode of the Futility Closet podcast we’ll describe Haffkine’s momentous work in India, which has been largely overlooked by history.
We’ll also consider some museum cats and puzzle over an endlessly energetic vehicle.

The Massachusetts Archives holds a 1775 bill from Paul Revere for “self and horse.”
It covers the period April 21-May 7, starting three days after the midnight ride. The provisional state government paid it.
“It seems at first blush incongruous, but then again, it’s not,” Massachusetts secretary of state William F. Galvin told the Bangor Daily News. “Even a revolutionary horse needs to be fed, not to mention Paul Revere himself.”
The Fall 1978 issue of Pi Mu Epsilon Journal included this problem, submitted by Pier Square. Four men are playing bridge. Their names are Banker, Waiter, Baker, and Farmer, and, as it happens, each man’s name is another man’s job. Mr. Baker’s partner is the baker, Mr. Banker’s partner is the farmer, and the waiter sits at Mr. Farmer’s right. Who is sitting at the banker’s left?