A puzzle from reader Steven Moore:
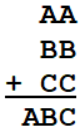
Find A, B, and C as distinct integers. There is only one solution.
A puzzle from reader Steven Moore:
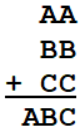
Find A, B, and C as distinct integers. There is only one solution.
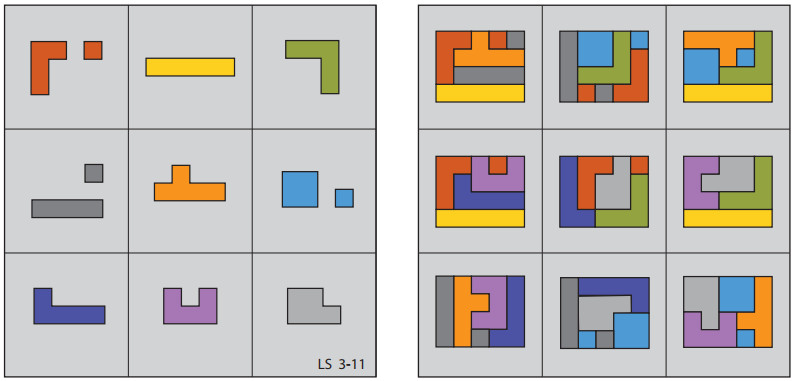
From Lee Sallows:
The traditional magic square is a square array of n×n distinct numbers, their magical property being that the sum of the n numbers occupying each row, column, and diagonal is the same. A variation on this theme that I introduced in 2011 is the geometric magic square in which distinct geometrical figures (usually planar shapes) occupy the cells of the array rather than numbers. The magical property enjoyed by such an array is then that the n shapes making up each row, column, and diagonal can be fitted together as in a jigsaw puzzle so as to yield (i.e. tile) a new compound shape that is the same in each case.
Beyond ‘ordinary’ geometric magic squares, it turns out that the combinative properties of shapes are such as to enable ‘magical’ constructions that are denied to analogous structures using numbers. For example, at left in the figure above is seen a 3×3 square of a kind that cannot be realized using distinct numbers rather than shapes. Note first that the square is to be understood as ‘toroidally-connected’, which is to say, as if inscribed on a torus. Its left-hand edge is then to be interpreted as adjacent to its right-hand edge and its top edge adjacent to its bottom edge. Its magical property is then that the four pieces contained within any 2×2 subsquare can be assembled to produce an identical shape, in this case a rectangle of size 4×5. In all there are nine such subsquares to be found in the square, as seen (again in a square) at right. Note that three of the pieces are disjoint, my attempts to produce a similar solution using nine unbroken pieces having failed. So whereas a 3×3 magic square, numerical or geometric, satisfies at least 8 separate conditions ( 3 rows + 3 columns + 2 diagonals), the square here shown satisfies one more.
(Thanks, Lee!)
In 2011, after attorney Walter Maksym had filed the same complaint three times, federal judge Diane Sykes threw out the case, noting that “[e]ach iteration of the complaint was generally incomprehensible and riddled with errors, making it impossible for the defendants to know what wrongs they were accused of committing.” As an example she cited this passage — a single sentence of 345 words:
That pursuant to the RICO Act, Defendants extortive activities constituted a Pattern of Racketeering activity and conspiracy involving violations of 1956(a)(1)(B)(ii), and 18 U.S.C. § 1341 (wire fraud—the use of interstate mail or wire facilities, here telephone and facsimile transmissions), or the causing of any of those things promoting unlawful activity), and 18 U.S.C. § 1951 (interference with commerce and extortion by using and threatening to use legitimate governmental powers to obtain an illegitimate objectives under color of official right by wrongful plan, extortion, intimidation and threat of force and/or other unlawful consequence and through fear and misuse of there office to obstruct, hinder, interfere with, and/or affect commerce and the use and enjoyment of Plaintiffs’ property and obtaining, as uniformed public officials payment for unwanted services to which they were not entitled by law, attempting to conceal from the United States of America their true and correct income and the nature thereof so obtained from Plaintiffs in order to attempt to evade paying lawful taxes thereon in violation of 26 U.S. § 7201, et. seq., thereby using the governmental powers with which they have been entrusted to gain personal or illegitimate rewards and payments which they knew or should have known were made and/or obtained in return for the colorable official acts as aforesaid, and knowing that the property involved in a financial transaction represents the proceeds of some form of unlawful activity, conducts or attempts to conduct such a financial transaction which in fact involves the proceeds of specified unlawful activity with the intent to promote the carrying on of specified unlawful activity all in violation of RICO and the other laws set forth herein, inter alia, as well as acts chargeable under any of the following provisions of the laws of the State of Illinois 720 ILCS 5/33-3(d) (official misconduct); 720 ILCS 5/1211 (criminal home invasion); 720 ILCS 5/19-4 (criminal trespass to a residence) 720 ILCS 5/19-4); (theft 720 ILCS 5/16 (a)(1)&(2) by knowingly obtaining or exerting unauthorized and/or through threat control over Plaintiff’s property as aforesaid.
Sykes found 23 sentences of 100 words or more in Maksym’s complaint, and added that “much of the writing is little more than gibberish.” Maksym blamed the problems on his recent cancer treatment, saying that he had an “impeccable record.”
See Running On.

Offered in 1950, the alarmingly named Gilbert U-238 Atomic Energy Laboratory was exactly that — a children’s chemistry set that included radioactive material, in this case four glass jars containing uranium-bearing (U-238) ore samples.
“Produces awe-inspiring sights!” read the catalog. “Enables you to actually SEE the paths of electrons and alpha particles traveling at speeds of more than 10,000 miles per SECOND! Electrons racing at fantastic velocities produce delicate, intricate paths of electrical condensation — beautiful to watch. Viewing Cloud Chamber action is closest man has come to watching the Atom!”
It sounds rather worse than it was — in 2020 IEEE Spectrum determined that the likely radiation exposure was “minimal, about the equivalent to a day’s UV exposure from the sun” if the samples were not removed from their containers, in accordance with the safety instructions.
Children were not the best market for a fairly sophisticated kit, and fewer than 5,000 were sold, but creator Alfred Carlton Gilbert didn’t go hungry — he’d also invented the Erector Set.
On Boxing Day 1927, the Thames sailing barge Lady Daphne entered the difficult waters of the Isles of Scilly and passed with seeming assurance among its many rocky hazards. At length she began to veer toward land, though, and the islanders dispatched a lifeboat, which caught up with the ship just as she beached herself safely on the island of Tresco.
The only living thing aboard was a canary in a cage. Daphne‘s skipper had been washed overboard, and the remaining two crew members had abandoned the barge off the Cornish coast. Unmanned, she had somehow sailed herself among the rocks to a patch of safe sand.

Just a little detail that I thought was interesting: Famously the moon appears larger when it’s near the horizon, but you can defeat this illusion by bending over and viewing it between your legs.
Why this works isn’t clear — possibly it’s because the image is inverted on the retina, or it may be an effect of inverting the body’s orientation.
(Stanley Coren, “The Moon Illusion: A Different View Through the Legs,” Perceptual and Motor Skills 75:3 [1992], 827-831; Atsuki Higashiyama and Kohei Adachi, “Perceived Size and Perceived Distance of Targets Viewed From Between the Legs: Evidence for Proprioceptive Theory,” Vision Research 46:23 [2006], 3961-3976.)

The largest known protein, titin, also has the longest name, under the method recommended by the International Union of Pure and Applied Chemistry. But the distinction is purely academic — at 189,819 characters, the full name is so spectacularly unwieldy that it can’t be considered a practically useful word.
Here’s a morose man reading the whole thing — it takes three hours.
Here’s a creepy fragment by English ghost story writer M.R. James, published shortly after his death in 1936 — he’s recalling a memory from his childhood, when, alone one day in his father’s Suffolk rectory, he had looked out upon a wooden gate in a grove of trees:
As was but right it was shut, and nobody was upon the path that led to it or from it. But as I said a while ago, there was in it a square hole giving access to the fastening; and through that hole, I could see — and it struck like a blow on the diaphragm — something white or partly white. Now this I could not bear, and with an access of something like courage — only it was more like desperation, like determining that I must know the worst — I did steal down and, quite uselessly, of course, taking cover behind bushes as I went, I made progress until I was within range of the gate and the hole. Things were, alas! worse than I had feared; through that hole a face was looking my way. It was not monstrous, not pale, fleshless, spectral. Malevolent I thought and think it was; at any rate the eyes were large and open and fixed. It was pink and, I thought, hot, and just above the eyes the border of a white linen drapery hung down from the brows.
There is something horrifying in the sight of a face looking at one out of a frame as this did; more particularly if its gaze is unmistakably fixed upon you. Nor does it make the matter any better if the expression gives no clue to what is to come next. I said just now that I took this face to be malevolent, and so I did, but not in regard of any positive dislike or fierceness which it expressed. It was, indeed, quite without emotion: I was only conscious that I could see the whites of the eyes all round the pupil, and that, we know, has a glamour of madness about it. The immovable face was enough for me. I fled, but at what I thought must be a safe distance inside my own precincts I could not but halt and look back. There was no white thing framed in the hole of the gate, but there was a draped form shambling away among the trees.
“Do not press me with questions as to how I bore myself when it became necessary to face my family again. That I was upset by something I had seen must have been pretty clear, but I am very sure that I fought off all attempts to describe it. Why I make a lame effort to do it now I cannot very well explain: it undoubtedly has had some formidable power of clinging through many years to my imagination. I feel that even now I should be circumspect in passing that Plantation gate; and every now and again the query haunts me: Are there here and there sequestered places which some curious creatures still frequent, whom once on a time anybody could see and speak to as they went about on their daily occasions, whereas now only at rare intervals in a series of years does one cross their paths and become aware of them; and perhaps that is just as well for the peace of mind of simple people.”
City A contains 20,000 people. One percent of these have one foot only and wear one shoe apiece. Half of the remaining people go barefoot, wearing no shoes at all, and the rest wear two shoes apiece.
In City B, 20 percent of the residents have one foot only and wear one shoe apiece. Of the remainder, half go barefoot and half wear two shoes apiece.
If 20,000 shoes are worn in City B, what is its population?

In desert conditions, helicopter rotors are sometimes surrounded by sparkling rings. When flying sand strikes the abrasion strips on the leading edges of the blades, clouds of eroded titanium particles ignite as they’re exposed to oxygen.
The effect is most visible at night when the aircraft is near the ground, but it’s been observed as high as 1700 feet. It’s named after Benjamin Kopp and Joseph Etchells, two soldiers killed in combat in Afghanistan in July 2009.