
In 1915 James Ferguson Smyth invited Hermann Helms to play a practice game at the Manhattan Chess Club. They had reached the position above when Helms, as Black, found a brilliant two-move mate. What is it?

In 1915 James Ferguson Smyth invited Hermann Helms to play a practice game at the Manhattan Chess Club. They had reached the position above when Helms, as Black, found a brilliant two-move mate. What is it?

In 1997 a series of eruptions by the nearby Soufrière Hills volcano buried most of Plymouth, Montserrat, making it uninhabitable.
The government was moved to the town of Brades, but nominally Plymouth remains the capital, making it the only ghost town that serves as the capital of a political territory.

On May 14, 2008, 19-year-old Brandon Swanson of Marshall, Minnesota, called his parents around 2 a.m. to say he’d driven his car into a ditch and asked them to pick him up. He said he wasn’t hurt and gave them his best estimate of his location.
His parents drove to meet him, keeping in touch by phone, but couldn’t find him. Each party flashed its headlights, but neither could see the other.
Finally Brandon told them he was going to walk toward some lights that he took to be the town of Lynd, 7 miles from Marshall. He named a bar there and asked his father to meet him in the parking lot, and his father began to drive there, talking to Brandon as he did.
Shortly after 2:30 a.m., 47 minutes into the call, Brandon suddenly interrupted himself with the words “Oh, shit!”, and the connection was lost. He has not been seen or heard from since.
Cell phone records showed that he’d been near Porter, 25 miles from the location he’d estimated. His car was found nearby, but years of searching have not found a body. The case remains unsolved.

In 1911 an exhausted man emerged from the wilderness north of Oroville, California. He was discovered to be the last of the Yahi, a people who had once flourished in the area but had been decimated by white settlers. In this week’s episode of the Futility Closet podcast we’ll describe Ishi’s sad history and his new life in San Francisco.
We’ll also consider the surprising dangers of baseball and puzzle over a forceful blackout.
A problem from the 1999 Russian Mathematical Olympiad:
Each cell of a 50×50 square is colored in one of four colors. Show that there exists a square which has cells of the same color as it directly above, directly below, directly to the left, and directly to the right of it (though not necessarily adjacent to it).

The elephant is no more wonderful than his biographers usually make him. It was to his lordly self that a railway accident was due on the Perak State Railway [Malaya] in September. The last train for the day was about three miles distant from its destination (Teluk Anson), and was running at about twenty miles an hour, when the fireman noticed something on the line. He called to the driver, who immediately shut off steam. Too late, however, for the train collided violently with a huge object, which proved to be a wild elephant that had strayed on to and was crossing the line at the time. The elephant had one of its legs broken, and half cut off; a part of the trunk was also cut off. The monster itself was thrown down the bank, where it soon died from loss of blood. The engine was also derailed.
— The Sketch, Jan. 16, 1895
I can find two stories of subsequent “duels” between elephants and locomotives on the same line. The Singapore Free Press and Mercantile Advertiser (1926) describes one that took place in 1897, and Forest and Stream has an account of one in 1900. Neither mentions the other, though, so I think perhaps they’re describing the same encounter.

Suppose you build a ship that can take you to Barnard’s Star. Should you depart today? Perhaps not: Our civilization might create a faster ship tomorrow that will overtake you on the journey. But clearly if you wait too long then you’ll simply lose out to an earlier ship. There must be some optimal waiting time that will deliver you to the star before any other pilot.
What is that time? “It has been shown that taking reasonable estimates for growth, an interstellar journey of 6 light years can best be made in about 635 years from now if growth continues at about 1.4% per annum,” writes researcher Andrew Kennedy. “At this point, the journey could be made in 145 years.”
(Andrew Kennedy, “Interstellar Travel: The Wait Calculation and the Incentive Trap of Progress,” Journal of the British Interplanetary Society 59:7 [2006], 239-246.)
“Belief in progress doesn’t mean belief in progress that has already occurred. That would not require belief.” — Kafka
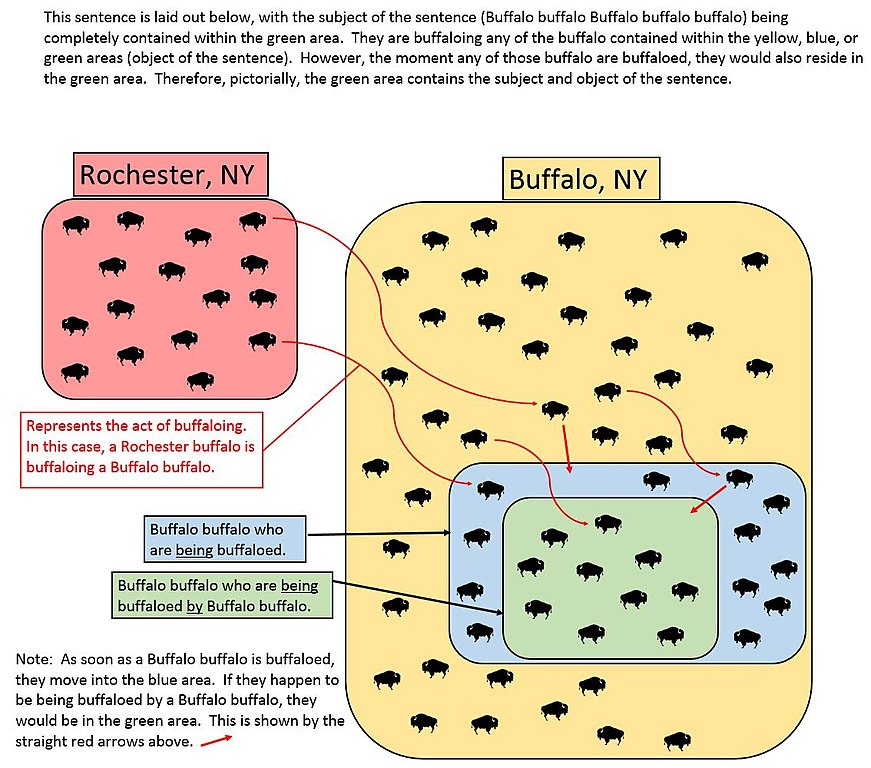
I had written about this back in 2006, but it’s worth mentioning again because someone has created this pellucid diagram: Buffalo buffalo Buffalo buffalo buffalo buffalo Buffalo buffalo is a grammatical English sentence. It means something like “Bison residing in Buffalo, New York, feeling themselves intimidated by their fellows, visit a similar fate upon yet others of their local ilk.”
I’d attributed it to linguist William J. Rapaport, but apparently it’s arisen independently at least three times, first (it is believed) by wordplay maven Dmitri Borgmann, in 1965.
Square roots:
EIGHTY-ONE has 9 letters.
ONE HUNDRED has 10 letters.
FIVE HUNDRED AND SEVENTY SIX has 24 letters.
Cube roots:
THIRTY-NINE THOUSAND THREE HUNDRED FOUR has 34 letters.
SIXTY-EIGHT THOUSAND NINE HUNDRED AND TWENTY-ONE has 41 letters.
ONE MILLION and ONE BILLION have 10 letters each, making them a sixth root and (in the United States) a ninth root word.
(Dave Morice, “Kickshaws,” Word Ways 30:2 [May 1997], 129-141.)
10/26/2020 UPDATE: Reader Hans Havermann has found many more, including this alarming specimen:
341183 = ONE HUNDRED SIXTY-NINE SENONAGINTILLION, FIVE HUNDRED FIVE QUINONAGINTILLION, SEVENTY-SEVEN QUATTUORNONAGINTILLION, FIFTY-ONE TRENONAGINTILLION, EIGHT HUNDRED SEVENTY DUONONAGINTILLION, SEVEN HUNDRED FIFTY-FOUR UNONAGINTILLION, SEVEN HUNDRED THIRTY-EIGHT NONAGINTILLION, SIX HUNDRED FIFTY-SIX NOVOCTOGINTILLION, TWO HUNDRED SEVENTY OCTOCTOGINTILLION, TWO HUNDRED NINETY-EIGHT SEPTENOCTOGINTILLION, SIX HUNDRED FORTY-SEVEN SEXOCTOGINTILLION, EIGHT HUNDRED FORTY-EIGHT QUINTOCTOGINTILLION, FOUR HUNDRED FOUR QUATTUOROCTOGINTILLION, EIGHT HUNDRED FIFTY-SIX TRESOCTOGINTILLION, SIX HUNDRED THIRTEEN DUOOCTOGINTILLION, EIGHT HUNDRED THIRTY-THREE UNOCTOGINTILLION, NINE OCTOGINTILLION, SEVEN HUNDRED SIXTY-FIVE NOVEMSEPTUAGINTILLION, EIGHT HUNDRED SIXTY-SEVEN OCTOSEPTUAGINTILLION, ONE HUNDRED FIFTY-THREE SEPTENSEPTUAGINTILLION, NINE HUNDRED SEVENTY-TWO SESEPTUAGINTILLION, EIGHT HUNDRED SEVENTY-EIGHT QUINSEPTUAGINTILLION, FIFTY-NINE QUATTUORSEPTUAGINTILLION, SEVEN HUNDRED SIX TRESEPTUAGINTILLION, EIGHT HUNDRED FIFTEEN DUOSEPTUAGINTILLION, TWO HUNDRED THIRTY-ONE UNSEPTUAGINTILLION, FOUR HUNDRED EIGHT SEPTUAGINTILLION, ONE HUNDRED FIFTY-FIVE NOVEMSEXAGINTILLION, FOUR HUNDRED EIGHTY-SIX OCTOSEXAGINTILLION, TWELVE SEPTENSEXAGINTILLION, TWO HUNDRED FORTY-SIX SESEXAGINTILLION, EIGHT HUNDRED EIGHTY-FIVE QUINSEXAGINTILLION, TWO HUNDRED FIFTY-SIX QUATTUORSEXAGINTILLION, FOUR HUNDRED NINETY-TWO TRESEXAGINTILLION, SEVEN HUNDRED FORTY-THREE DUOSEXAGINTILLION, FIVE HUNDRED FIFTY-FIVE UNSEXAGINTILLION, ONE HUNDRED FORTY-ONE SEXAGINTILLION, EIGHT HUNDRED TWENTY-FIVE NOVEMQUINQUAGINTILLION, SEVEN HUNDRED FORTY-SIX OCTOQUINQUAGINTILLION, ONE HUNDRED SEVENTY-ONE SEPTENQUINQUAGINTILLION, NINE HUNDRED THIRTY-TWO SEXQUINQUAGINTILLION, ONE HUNDRED SIXTY-SIX QUINQUINQUAGINTILLION, FOUR HUNDRED THREE QUATTUORQUINQUAGINTILLION, THIRTY-TWO TRESQUINQUAGINTILLION, SIX HUNDRED TWENTY-FOUR DUOQUINQUAGINTILLION, ONE HUNDRED FORTY-SIX UNQUINQUAGINTILLION, ONE HUNDRED TWENTY-FIVE QUINQUAGINTILLION, EIGHT HUNDRED TWO NOVEMQUADRAGINTILLION, EIGHT HUNDRED FIFTY-EIGHT OCTOQUADRAGINTILLION, ONE HUNDRED SEVENTY-NINE SEPTENQUADRAGINTILLION, ONE HUNDRED FIFTY-SIX SEXQUADRAGINTILLION, ONE HUNDRED TWENTY-FOUR QUINQUADRAGINTILLION, NINE HUNDRED FIFTY-FOUR QUATTUORQUADRAGINTILLION, NINE HUNDRED ELEVEN TRESQUADRAGINTILLION, TWO HUNDRED FIFTEEN DUOQUADRAGINTILLION, NINE HUNDRED SIXTY-SIX UNQUADRAGINTILLION, NINE HUNDRED TWELVE QUADRAGINTILLION, EIGHT HUNDRED THREE NOVEMTRIGINTILLION, SIX HUNDRED SIXTY-EIGHT OCTOTRIGINTILLION, SEVEN HUNDRED SIXTY-THREE SEPTRIGINTILLION, ONE HUNDRED EIGHTY-THREE SEXTRIGINTILLION, SEVEN HUNDRED NINETY-SIX QUINTRIGINTILLION, NINETY QUATTUORTRIGINTILLION, SEVEN HUNDRED TRESTRIGINTILLION, FIVE HUNDRED EIGHTY-SIX DUOTRIGINTILLION, ONE HUNDRED FORTY-ONE UNTRIGINTILLION, SIX HUNDRED FIFTY-FOUR TRIGINTILLION, SIX HUNDRED EIGHT NOVEMVIGINTILLION, SEVEN HUNDRED FIFTY-THREE OCTOVIGINTILLION, SIX HUNDRED FOURTEEN SEPTENVIGINTILLION, THREE HUNDRED FOUR SEXVIGINTILLION, SEVEN HUNDRED NINETY-FIVE QUINVIGINTILLION, SIX HUNDRED FORTY-FOUR QUATTUORVIGINTILLION, THREE HUNDRED SIXTY-FIVE TREVIGINTILLION, EIGHT HUNDRED NINETY-SEVEN DUOVIGINTILLION, EIGHT HUNDRED SEVENTEEN UNVIGINTILLION, FIVE HUNDRED EIGHTY-TWO VIGINTILLION, FOUR HUNDRED FIFTY-FIVE NOVEMDECILLION, FOUR OCTODECILLION, SIX HUNDRED FORTY-FIVE SEPTENDECILLION, NINE HUNDRED SEVEN SEXDECILLION, FOUR HUNDRED EIGHTY QUINDECILLION, EIGHT HUNDRED THIRTY-SEVEN QUATTUORDECILLION, ONE HUNDRED FORTY-FOUR TREDECILLION, TWO HUNDRED TWENTY-FIVE DUODECILLION, EIGHT HUNDRED EIGHTY-ONE UNDECILLION, SIX HUNDRED SEVEN DECILLION, THREE HUNDRED FIFTY-TWO NONILLION, FIVE HUNDRED FORTY-THREE OCTILLION, FOUR HUNDRED NINE SEPTILLION, TWO HUNDRED SEVENTY-NINE SEXTILLION, ONE HUNDRED EIGHTY-EIGHT QUINTILLION, SEVEN HUNDRED SEVENTY-SIX QUADRILLION, FORTY-EIGHT TRILLION, THREE HUNDRED NINETY-FOUR BILLION, SEVEN HUNDRED SEVENTY-ONE MILLION, EIGHT HUNDRED EIGHT THOUSAND, THREE HUNDRED THIRTY-ONE
The name of that number contains 3,411 letters.
(Thanks, Hans.)