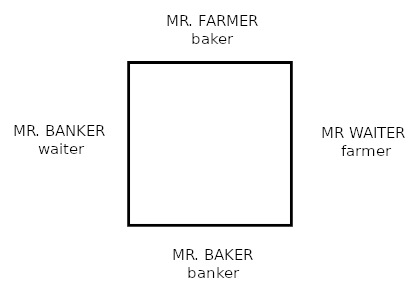
The Fall 1978 issue of Pi Mu Epsilon Journal included this problem, submitted by Pier Square. Four men are playing bridge. Their names are Banker, Waiter, Baker, and Farmer, and, as it happens, each man’s name is another man’s job. Mr. Baker’s partner is the baker, Mr. Banker’s partner is the farmer, and the waiter sits at Mr. Farmer’s right. Who is sitting at the banker’s left?
Unquote
“To convince any man against his will is hard, but to please him against his will is justly pronounced by Dryden to be above the reach of human abilities.” — Samuel Johnson
“Thou canst not joke an Enemy into a Friend; but thou may’st a Friend into an Enemy.” — Ben Franklin
Seeing Red
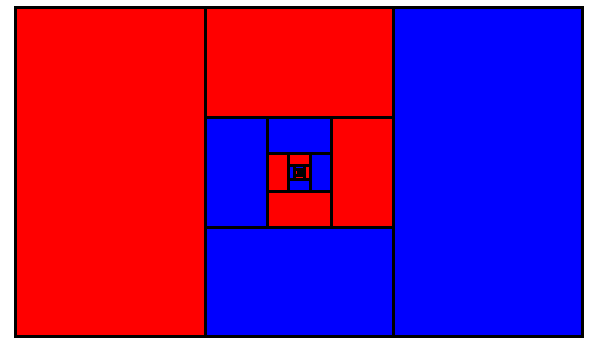
University of Waterloo mathematician Ross Honsberger chose this problem for his 2004 collection Mathematical Delights; it’s a generalization of a problem that Robert Gebhardt had offered in the Fall 1999 issue of Pi Mu Epsilon Journal. Paint the outside of an n × n × n cube red, then chop it into n3 unit cubes. Put the unit cubes in a box, mix them up thoroughly, withdraw one at random, and throw it across a table. What’s the probability that it comes to rest with a red face on top?
Nowheresville

In September 2008, Mike Nolan, head of web services at Edge Hill University in Ormskirk, England, noticed something strange on Google Maps. “I grew up in the area and spotted on the map one day that it said ‘Argleton’,” he told the Guardian. “But it’s just a farmer’s field close to the village hall and playing fields. I think a footpath goes across the field, but that’s all.”
Bloggers began to discuss the nonexistent town, which found its way into other services that used Google’s data: Employment agencies, weather services, and letting agents began to cite Argleton in their listings, reassigning real people and businesses to the phantom settlement because of its claimed location.
Was it a joke? A placeholder? A misspelling? Whatever it was, it had disappeared again by May 2010. Google would say only that it experiences “occasional errors” and that it gets its mapping information from a Dutch company called Tele Atlas (whose spokesperson would add only, “I really can’t explain why these anomalies get into our database”).
Danny Dorling, president of the Society of Cartographers, said, “I would bet that this is an innocent mistake. In other words, it was not intentionally inserted to catch out anyone infringing the map’s copyright, as some are saying. But the bottom line is that we don’t know what mapping companies do to protect their maps or to hide secret locations, as some are obligated to do.”
Cutting Cake
In the College Mathematics Journal in 2001, Rick Mabry published this “proof without words” that
He gives a charming explanation here.
(Rick Mabry, “Mathematics Without Words,” College Mathematics Journal 32:1 [January 2001], 19.)
Best Friends

Hence it is that the moral character of a man eminent in letters or in the fine arts is treated, often by contemporaries, almost always by posterity, with extraordinary tenderness. … These friendships are exposed to no danger from the occurrences by which other attachments are weakened or dissolved. … Plato is never sullen. Cervantes is never petulant. Demosthenes never comes unseasonably. Dante never stays too long. No difference of political opinion can alienate Cicero. No heresy can excite the horror of Bossuet. Nothing, then, can be more natural than that a person endowed with sensibility and imagination should entertain a respectful and affectionate feeling towards those great men with whose minds he holds daily communion.
— Thomas Macaulay, An Essay on Francis Bacon, 1837
First Things First

It is a traditional axiom of medicine that health is the absence of disease. What is a disease? Anything that is inconsistent with health. If the axiom has any content, a better answer can be given. The most fundamental problem in the philosophy of medicine is, I think, to break the circle with a substantive analysis of either health or disease.
— Christopher Boorse, “Health as a Theoretical Concept,” Philosophy of Science 44:4 (1977), 542-573
“The Individual and the World”

There is an eternal antagonism of interest between the individual and the world at large. The individual will not so much care how much he may suffer in this world provided he can live in men’s good thoughts long after he has left it. The world at large does not so much care how much suffering the individual may either endure or cause in this life, provided he will take himself clean away out of men’s thoughts, whether for good or ill, when he has left it.
— Samuel Butler, Notebooks
The Presidents’ Tree
In August 1865, Maryland farmer Samuel M’Closky Fenton carved this grid into an American beech in Takoma Park:
N L O C N I L M L I N C O L N L O C N I L M A M L I N C O L O C N I L M A H A M L I N C O C N I L M A H A H A M L I N C N I L M A H A R A H A M L I N I L M A H A R B R A H A M L I L M A H A R B A B R A H A M L I L M A H A R B R A H A M L I N I L M A H A R A H A M L I N C N I L M A H A H A M L I N C O C N I L M A H A M L I N C O L O C N I L M A M L I N C O L N L O C N I L M L I N C O L N
He intended it as a memorial to Abraham Lincoln, who had been assassinated that April. Starting at the central A and following a jagged path toward any of the corner Ns will spell out the fallen president’s name.
Fenton also carved the name of every American president to date. In 1948 the tree was enclosed in an iron fence and dedicated “as a living memorial to men who gave their lives for their country in the war of 1861-1865.”
In a Word
philobiblist
n. a lover of books
Created by Slovakian artist Matej Kren, the Idiom Installation in Prague’s municipal library seems to present an infinite tower of books, thanks to some conveniently placed mirrors.
It debuted at the São Paulo International Biennial in 1995 and moved permanently Prague in 1998.