
In 1853, a lady at a social dinner challenged explorer Jacques Arago to compose an account of his circumnavigation without using the letter A.
Allegedly she thanked him without using the letter C.

In 1853, a lady at a social dinner challenged explorer Jacques Arago to compose an account of his circumnavigation without using the letter A.
Allegedly she thanked him without using the letter C.

“Whoopee! Man, that may have been a small one for Neil, but that’s a long one for me!” — Pete Conrad, after becoming the third human to set foot on the moon

Suppose … for a moment, all existing space to be bounded, and that a man runs forward to the uttermost borders, and stands upon the last verge of things, and then hurls forward a winged javelin,– suppose you that the dart, when hurled by the vivid force, shall take its way to the point the darter aimed at, or that something will take its stand in the path of its flight, and arrest it? For one or other of these things must happen. There is a dilemma here that you never can escape from.
— Lucretius, De rerum natura

University of Cambridge mathematician Matthew Scroggs has post his annual Christmas puzzle: Behind each day in an advent calendar lies a puzzle with a three-digit answer. Combined, the answers reveal a series of compass directions that lead to Santa’s house. Ten randomly selected people who solve all the puzzles and find Santa’s house will receive prizes. More info here.

In 1903 Robert Falcon Scott made an odd discovery in the Dry Valleys of Antarctica:
[W]e have seen no living thing, not even a moss or a lichen; all that we did find, far inland amongst the moraine heaps, was the skeleton of a Weddell seal, and how that came there is beyond guessing. It is certainly a valley of the dead; even the great glacier which once pushed through it has withered away.
It appears that periodically a crabeater, Weddell, or leopard seal finds its way inland from McMurdo Sound and the Ross Sea and perishes in the punishing environment of the dry valleys, an extreme desert. There the dry conditions mummify its corpse, preserving it in some cases for thousands of years.
Some mummies have been found as much as 41 miles inland and as high as 5,900 feet above sea level, reflecting a heroic effort to find the sea. Mercifully the phenomenon is relatively rare, with a seal becoming lost only once every 4 to 8 years.
“I think it is all right to argue sometimes.”
“I disagree!”
(From Raymond Smullyan.)
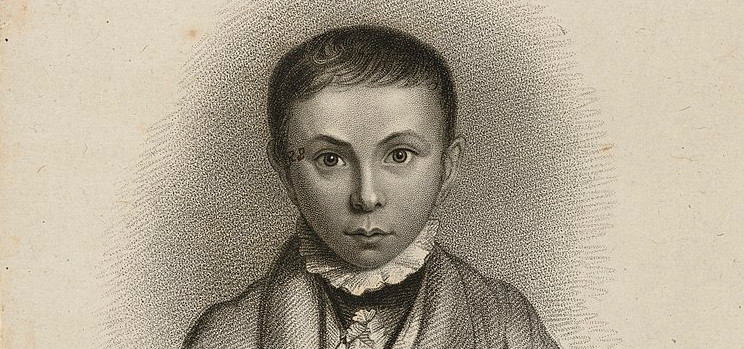
George Parker Bidder was born with a surprising gift: He could do complex arithmetic in his head. His feats of calculation would earn for him a university education, a distinguished career in engineering, and fame throughout 19th-century England. In this week’s episode of the Futility Closet podcast, we’ll describe his remarkable ability and the stunning displays he made with it.
We’ll also try to dodge some foul balls and puzzle over a leaky ship.
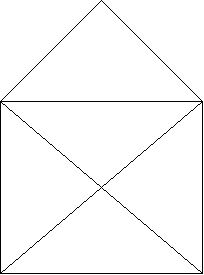
Can you draw this figure without lifting your pencil from the paper?

Imaginary distinctions are often drawn between beliefs which differ only in their mode of expression;– the wrangling which ensues is real enough, however. To believe that any objects are arranged as in Fig. 1, and to believe that they are arranged as in Fig. 2, are one and the same belief; yet it is conceivable that a man should assert one proposition and deny the other. Such false distinctions do as much harm as the confusion of beliefs really different, and are among the pitfalls of which we ought constantly to beware, especially when we are upon metaphysical ground. One singular deception of this sort, which often occurs, is to mistake the sensation produced by our own unclearness of thought for a character of the object we are thinking. Instead of perceiving that the obscurity is purely subjective, we fancy that we contemplate a quality of the object which is essentially mysterious; and if our conception be afterward presented to us in a clear form we do not recognize it as the same, owing to the absence of the feeling of unintelligibility. So long as this deception lasts, it obviously puts an impassable barrier in the way of perspicuous thinking; so that it equally interests the opponents of rational thought to perpetuate it, and its adherents to guard against it.
— Charles Sanders Peirce, “Illustrations of the Logic of Science: How to Make Our Ideas Clear,” Popular Science Monthly, January 1878

Founded in 1957, catalog showroom Best Products distinguished itself with highly unorthodox facades, designed by architect James Wines for nine retail facilities across the United States. This one, the “Indeterminate Facade” in Houston, Texas, was said to have appeared in more books on 20th-century architecture than photographs of any other modern structure. The company eventually went bankrupt, and most of the buildings have been redesigned or demolished, but one in Richmond, Va., with a forest in its entryway, is now home to a Presbyterian church.
See more at Archilaces.