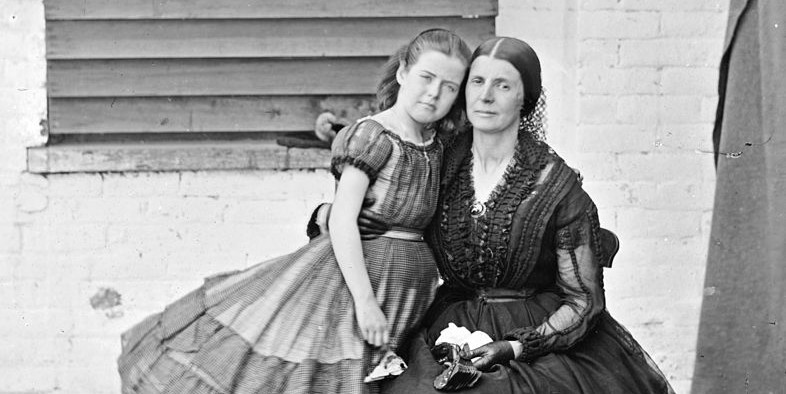
As the Civil War fractured Washington D.C., socialite Rose O’Neal Greenhow coordinated a vital spy ring to funnel information to the Confederates. In this week’s episode of the Futility Closet podcast we’ll describe one of the war’s most unlikely spies, and her determination to aid the South.
We’ll also fragment the queen’s birthday and puzzle over a paid game of pinball.