British maze designer Randoll Coate produced this tribute to Jorge Luis Borges — a labyrinth of hedges shaped like an open book and spelling out the author’s name. (The original maze is in the writer’s native Argentina; Coate donated the copy above to Borges’ foundation in Venice.)
“Five years before Borges died, I had a dream in which I heard that Borges had just died,” the designer recalled. “And I thought to myself, I must make sure that Borges is not memorialized with one of those terrible statues — a depiction of angels or something. He has to be honored with something truly Borgesian, in other words, a labyrinth. That’s when I began to design it and think about it and dream up a shape for it — an extraordinary labyrinth for a man with an extraordinary mind.”

(From Francesca Tatarella, Labyrinths & Mazes, 2016.)
11/29/2017 UPDATE: Coate’s design is more sophisticated than I’d realized — from reader Daniël Hoek:
“The maze also contains a tiger, a walking stick, a question mark, the initials MK of his wife, and two hourglasses that spell the number of years Borges lived (’86’). After some effort I think I found all of those (the tiger is very cool once you find it –– you need to rotate the plan as in the attached image)”:
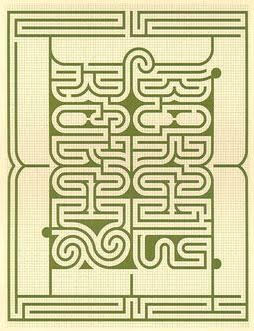
“PS. Another interesting tidbit: the maze in ‘The Garden of Forking Paths’ has the feature that you can make it through by going left at every turn. Starting at the top entrance and discounting any forced turns, that is also true of this maze, although that is a boring route that takes you around the maze and not through the center.”