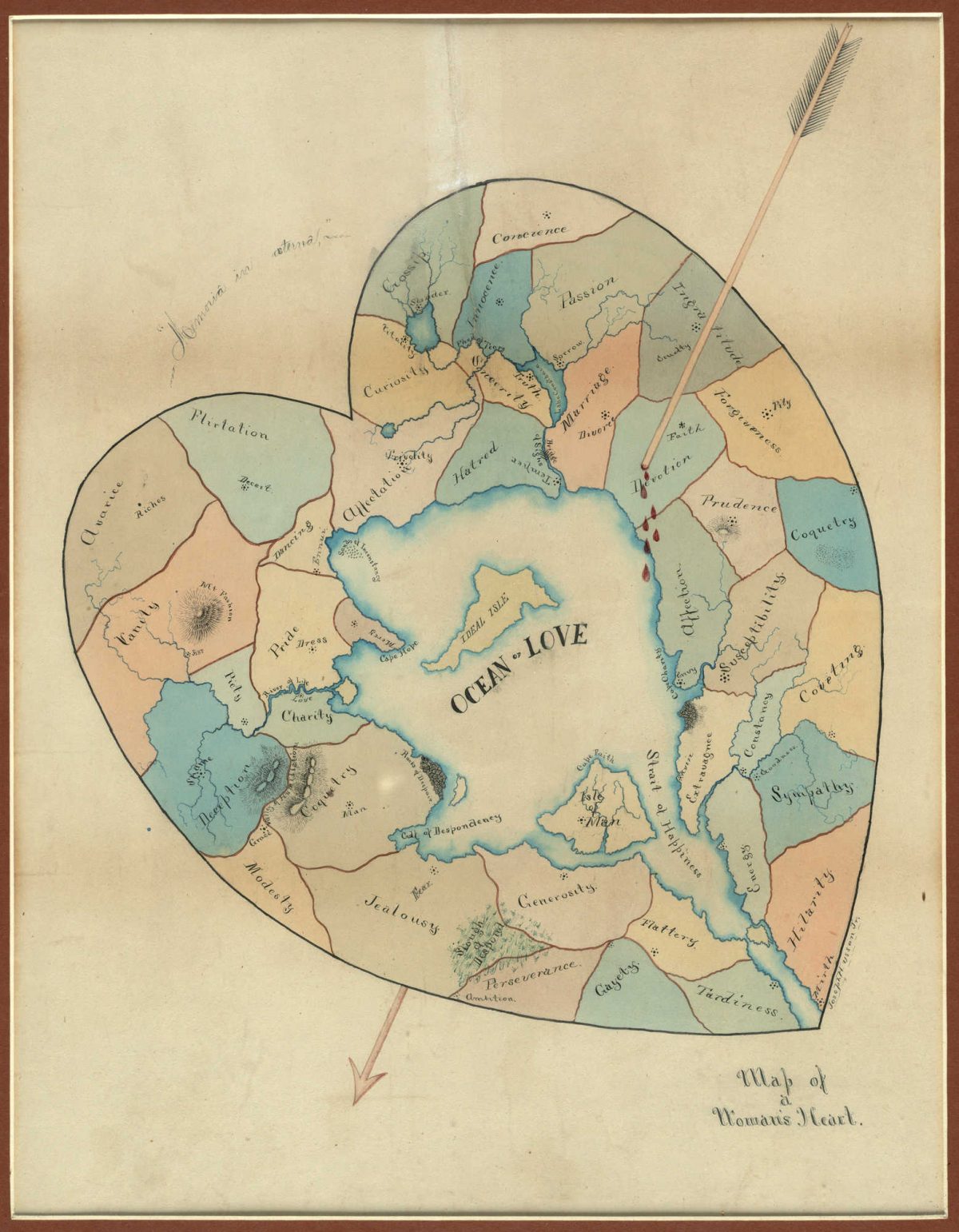
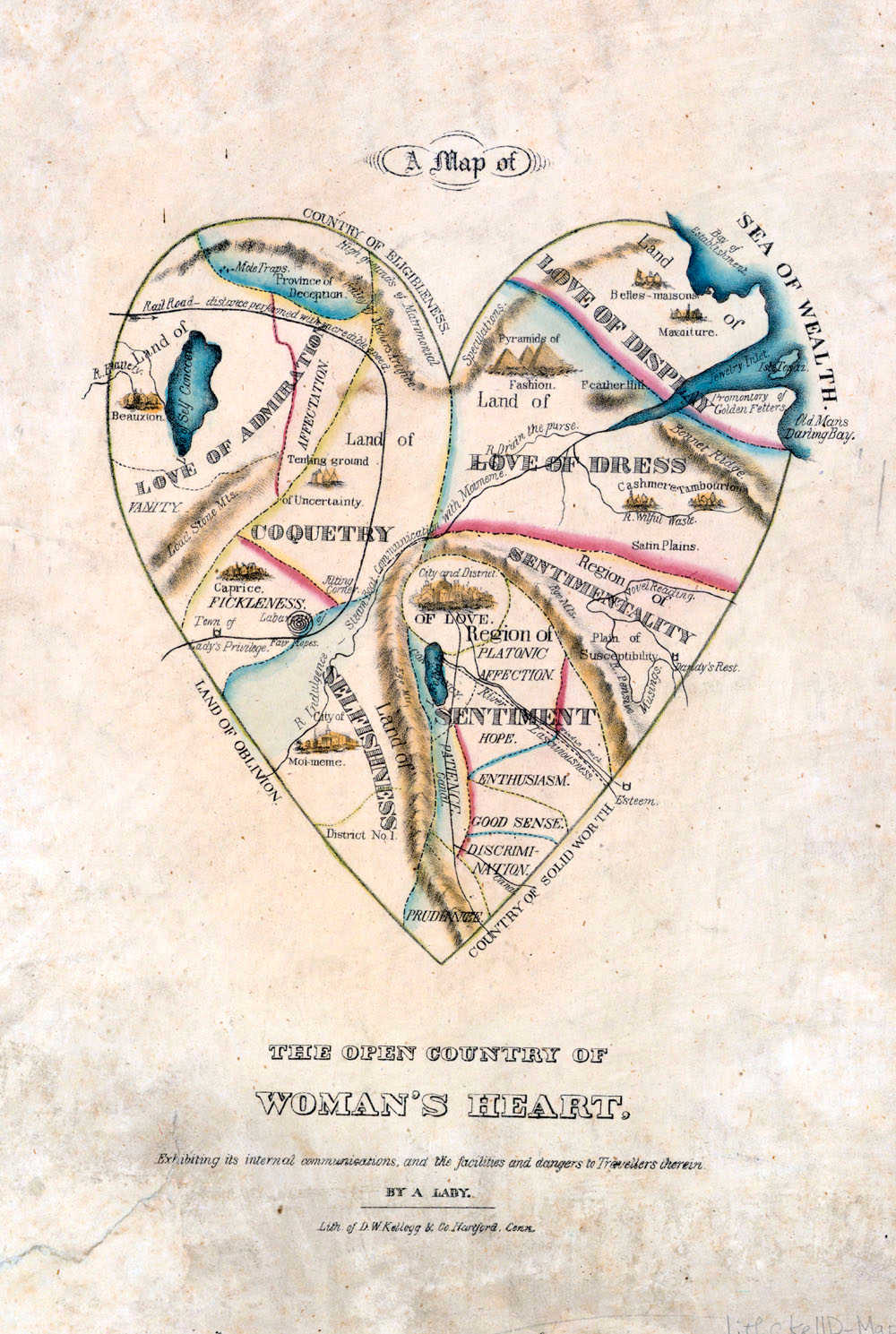
Sixteenth-century England had some singularly inept bowmen:
In 1552, at about 3 pm on the 28th October, Henry Pert, gentleman, went out to play at Welbeck [Nottinghamshire] and drew his bow so fully with an arrow in it that he lodged the arrow in his bow. Afterwards, intending to make the arrow climb straight into the air, he shot the arrow from his bow while leaning slightly over the bow. Because his face was directly over the arrow as it climbed upwards it struck him over his left eyelid and into his head to the membrane of his brain. Thus the said arrow, worth one farthing, gave him a wound of which he immediately languished, and lay languishing until 12 pm on 29th October when he died, by misadventure.
In The Romance of Archery, historian Hugh D.H. Soar adds, “The coroner was sufficiently curious about this circumstance to take matters a little further. He inquired how this accident could happen and was told by knowledgeable colleagues that the unfortunate Henry was notable for using too short an arrow and regularly drawing it inside his bow.”