Law and Ordure

Chicago artist Jerzy Kenar put up this bronze statue in front of his East Village home as a gentle reminder: “I hoped it would motivate dog owners to pick up after their pets.”
When the water’s running it looks even more realistic than this. But both mayor Richard M. Daley and Father Michael Pfleger, pastor of St. Sabina Church, attended the unveiling in 2005.
Kenar says that the statue, at 1003 North Wolcott Avenue, is intended to be whimsical, and that most visitors take it in that spirit, posing and even drinking from the fountain. “Only one little old lady didn’t get the joke,” he said.
He also designed the Black History Fountain near St. Sabina … so this one is sometimes called his “number two fountain.”
(From Greg Borzo, Chicago’s Fabulous Fountains, 2017.)
For the Record
Western Kentucky University geoscientist John All was traversing Nepal’s Mount Himlung in May 2014 when the ice collapsed beneath him and he fell into a crevasse, dislocating his shoulder and breaking some ribs. He landed on a ledge, but now he faced a 70-foot climb back to the surface alone without the use of his right arm or upper leg.
“That’s when I pulled my research camera out and started talking to myself about all my options,” he told National Geographic. “I take photos of everything I do because, if I’m working in Africa and I need to recall a detail, that’s going to be the best way to do it. I was also thinking about my mom and my friends and family and realized that just talking wouldn’t convey what was happening to me nearly as well. So I started recording things.”
“It probably took me four or five hours to climb out,” he said. “I kept moving sideways, slightly up, sideways, slightly up, until I found an area where there was enough hard snow that I could get an ax in and pull myself up and over. I knew that if I fell at any time in that entire four or five hours, I, of course, was going to fall all the way to the bottom of the crevasse. Any mistake, or any sort of rest or anything, I was going to die.”
After reaching the top he rolled as much as walked back to his tent, called for help, and waited 16 hours for a helicopter to arrive. He wrote later, “I had dug myself out of my own grave.”
Introductions

A poem by Louis Phillips: “If the Modern Artist Ralph Goings Had Met the Poet E.E. Cummings”:
Goings?
Cummings?
Cummings,
Goings.
Goings,
Cummings.
Going,
Goings?
Yep.
Cummings,
Going?
Nope.
Double Talk

In talking about superheroes, these sentences seem natural and right:
(la) Clark Kent went into the phone booth and Superman came out.
(2a) Superman leapt over tall buildings.
(3a) Superman is more successful with women than Clark Kent.
(4a) Batman wears a mask.
But these seem inappropriate or wrong:
(lb) Clark Kent went into the phone booth and Clark Kent came out.
(2b) Clark Kent leapt over tall buildings.
(3b) Clark Kent is more successful with women than Clark Kent.
(4b) Bruce Wayne wears a mask.
Why is this? If we know that Superman is Clark Kent, then those terms should be interchangeable — a statement about Superman is a statement about Clark Kent; they’re the same person.
“At least in some conversational scenarios, utterances of (la)-(4a) strike us as true, and utterances of (lb) (4b) appear to be false,” writes University of Nottingham philosopher Stefano Predelli. “(3a), for instance, seems just the right thing to say when discussing women’s fascination with men in blue leotard; utterances of (3b), on the other hand, seem trivially false. Similarly, during a discussion of why the famed superhero never engages in extraordinary feats when playing the part of the timid journalist, utterances of (2a) seem unobjectionable, but utterances of (2b) will not do.” Why?
(Stefano Predelli, “Superheroes and Their Names,” American Philosophical Quarterly 41:2 [April 2004], 107-123.)
Spelling It Out
In the 17th century, French architect Thomas Gobert planned 12 churches whose forms spelled out the words LOVIS LE GRAND (where each letter is doubled mirrorwise, for symmetry):

In 1775 Johann David Steingruber designed a castle whose floor plan formed the initials of Prince Christian Carl Friedrich Alexander of Anspach:
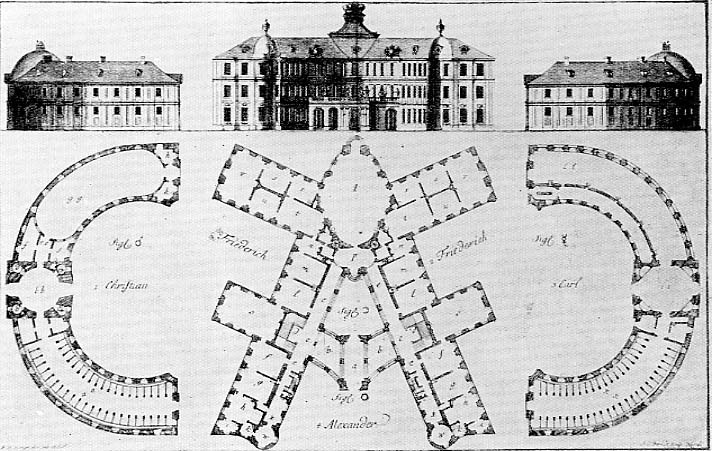
And in 1774 Anton Glonner designed a Jesuit college based on the name of Christ (IHS, the first three letters of Jesus’ name in Greek):
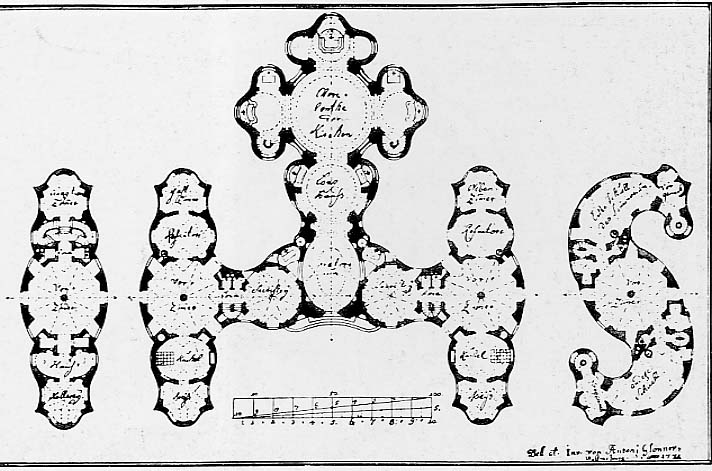
The H contained the kitchen, the dining room, and the sacristy, and the S contained the schoolrooms.
(From Ulrich Conrads and Hans G. Sperlich, The Architecture of Fantasy, 1962.)
Case Closed

“Witchfinder general” Matthew Hopkins hanged 300 women during the English Civil War, accounting for perhaps 60 percent of all executions for witchcraft at that time. After days of starvation, sleep deprivation, and forced walking, the accused women produced some extraordinary confessions:
Elizabeth Clark, an old, one-legged beggar-woman, gave the names of her ‘imps’ as ‘Holt,’ a ‘white kitling;’ ‘Jarmara,’ a ‘fat spaniel’ without legs; ‘Sacke and Sugar,’ a ‘black rabbet;’ ‘Newes,’ a ‘polcat;’ and ‘Vinegar Tom,’ a greyhound with ox-head and horns. Another called her ‘imps’ ‘Ilemauzar’ (or ‘Elemauzer’), ‘Pyewackett,’ ‘Pecke in the Crowne,’ and ‘Griezzell Greedigutt.’
This proved their guilt, Hopkins said — these were names “which no mortal could invent.”
Math Notes
121213882349 = (1212 + 1388 + 2349)3
128711132649 = (1287 + 1113 + 2649)3
162324571375 = (1623 + 2457 + 1375)3
171323771464 = (1713 + 2377 + 1464)3
368910352448 = (3689 + 1035 + 2448)3
Podcast Episode 166: A Dangerous Voyage

After Japan invaded the Philippines in 1941 two American servicemen hatched a desperate plan to sail 3,000 miles to Allied Australia in a 20-foot wooden fishing boat. In this week’s episode of the Futility Closet podcast we’ll join Rocky Gause and William Osborne as they struggle to avoid the Japanese and reach safety.
We’ll also tell time in Casablanca and puzzle over a towing fatality.
Alchemy
Mike Keith found this amazing correspondence in 2004. The two 6×6 squares below contain 72 different entries from the periodic table of the elements:
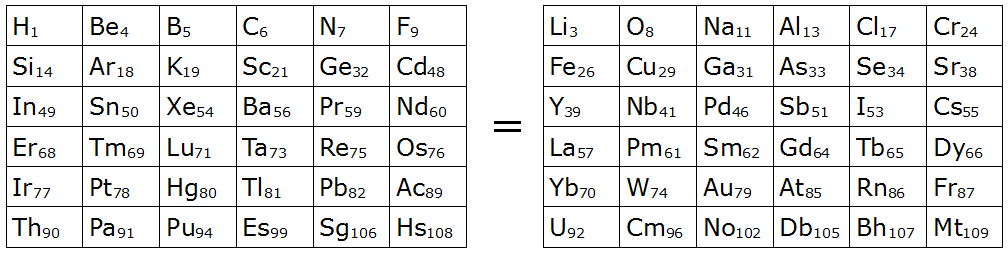
The two squares are equal in three different ways:
- If you spell out the name of each element listed (hydrogen, beryllium, etc.), the square on the left is an anagram of the square on the right.
- The sum of the atomic numbers of the 36 elements on the left (2019) equals the sum of those on the right.
- If you replace each symbol with its alphabetic score (where A=1, B=2, etc.; e.g. Li = L + I = 12 + 9 = 21), then the sum of the scores on the left (737) equals that of those on the right.
Keith writes, “The next largest pair of triply-equal squares like this would be 7×7 in size, containing a total of 98 different elements, [and] it seems quite unlikely that 98 of them could be so arranged. If this is true then the 6×6 pair presented here is the largest possible (at least for now, until many more new chemical elements have been discovered and named).”
(Mike Keith, “A Magical Pair of 6×6 Chemical Squares,” Word Ways, February 2004.)
