How to escape the police while carrying a coil of duct tubing.
Adam’s Bridge

A curious chain of limestone shoals extends between India and Sri Lanka, possibly the remains of a land connection between the two. The sea between the two landmasses is called Sethusamudram (“Sea of the Bridge”), and early British maps refer to it as Adam’s Bridge. How and when the structure evolved are still sources of controversy among geologists, but historical records suggest that it was passable on foot until a cyclone deepened the channel in the 1400s.
Appealing to NASA satellite images, some sources contend that the bridge was created by Rama to rescue his kidnapped wife Sita, as described in Hindu theology, perhaps with the aid of a human army. NASA delicately observes that this interpretation “is certainly not ours. … Remote sensing images or photographs from orbit cannot provide direct information about the origin or age of a chain of islands, and certainly, cannot determine whether humans were involved in producing any of the patterns seen.”
Grant and the Mule

From Judge Jacob W. Wilkin’s “Personal Reminiscences of General U.S. Grant,” 1907:
One day while riding on the lines, he saw a teamster beating a mule, and riding up to him, ordered him to stop. Wearing an army blouse without shoulder straps, the man did not recognize him and not very politely told him to mind his own business, using profane language, whereupon Grant told his orderly to arrest him and bring him to headquarters. He was turned over to me with orders to tie him up by the thumbs. When the fellow realized that he had used insulting language to General Grant he was the most humiliated man imaginable and protested he did not know it was General Grant. His punishment lasted but a little while and because of my sympathy, was not the most severe of the kind, when I was directed to bring him up to the headquarters tent and there he renewed his protestation that he did not know it was the general he was talking to and that he would not under any circumstances have insulted him. But the general said, ‘You don’t understand, it was not I that was hurt, it was the mule. I could defend myself but the poor dumb animal could say or do nothing for its own protection.’
“He dismissed the culprit with the admonition that he would be closely watched and if again found abusing his team, he would be summarily dealt with.”
From Beyond

From the St. Louis Post-Dispatch, via the Ohio Law Reporter, Aug. 17, 1908: During a dispute over a will in Vienna, a phonograph record was introduced into evidence so that the dead woman herself could explain her intentions, which she’d recorded during her lifetime:
Prof. Sulzer stated that he had a phonographic record that would settle beyond question the point in dispute and asked the court’s permission to introduce it as evidence. The permission was granted and Mme. Blaci, the decedent, told in her own voice of her affection for her brother and his family and announced her intention of providing before her death so that her nephew, Heinrich, would be well cared for after she had passed away.
Heinrich testified that the record was made on the twenty-first anniversary of his birth. Mme. Blaci, he told the judge, had said at the time that she wanted the words she had spoken to her brother, Heinrich’s father, put on record as a souvenir of her affection that could be handed down to her nephew.
“After hearing the record, the court immediately awarded Heinrich $120,000 as his share of the estate, which was the full amount claimed by him.”
“The Elephant Who Walked to Manchester”

In 1872, as he prepared to retire in Edinburgh, English menagerie owner Alexander Fairgrieve auctioned off his remaining attractions in the Waverley Market. The largest lot was Maharajah, an Indian elephant 7 feet tall with 20-inch tusks. The winning bid, £680, came from James Jennison, proprietor of the Belle Vue Gardens near Manchester, who was expanding his zoological collection. The elephant rebelled at entering a horse box on the Northern British Railway, so his keeper, Lorenzo “Lion Tamer” Lawrence, simply walked his charge to Manchester.
The unlikely pair covered 200 miles in 10 days, arriving on April 20, and the celebrated animal, “having travelled by road from Scotland, via Carlisle, Kendal, Lancaster, Preston and Bolton,” was installed in a temporary glass-roofed elephant house. In the ensuing years he would walk among the visitors, ridden by thousands of children and starring in spectacles such as “Napoleon Crossing the Alps” in the city’s May Day and Whit parades. He died of pneumonia in 1882 at the age of 18.
Heywood Hardy’s 1875 painting A Disputed Toll, above, records an event that probably never happened — it’s said that during their journey, while Lawrence was arguing with a parsimonious gatekeeper, Maharajah simply lifted the gate from its hinges. Accurate or not, the memorable painting now hangs in the Manchester Art Gallery.
Mr. Big

Epithets used to describe former North Korean leader Kim Jong-il in state media:
- Superior Person
- Dear Leader
- Respected Leader
- Wise Leader
- Brilliant Leader
- Unique Leader
- Dear Leader, Who Is a Perfect Incarnation of the Appearance That a Leader Should Have
- Commander-in-Chief
- Great Leader
- Father of the People
- Sun of the Communist Future
- Shining Star of Paektu Mountain
- Guiding Sun Ray
- Leader of the Revolutionary Armed Forces
- Guarantee of the Fatherland’s Unification
- Symbol of the Fatherland’s Unification
- Fate of the Nation
- Beloved Father
- Leader of the Party, the Country, and the Army
- Great Leader of our Party and of our Nation
- Great General
- Beloved and Respected General
- Great Leader
- Beloved and Respected Leader
- Ever-Victorious, Iron-Willed Commander
- Sun of Socialism
- Sun of the Nation
- The Great Sun of Life
- Great Sun of The Nation
- Father of the Nation
- World Leader of the 21st Century
- Peerless Leader
- Bright Sun of the 21st Century
- Great Sun of the 21st Century
- Leader of the 21st Century
- Amazing Politician
- Great Man, Who Descended From Heaven
- Glorious General, Who Descended From Heaven
- Supreme Leader of the Nation
- Bright Sun of Juche
- Leader of the Party and the People
- Great Marshal
- Invincible and Triumphant General
- Dear Father
- Guiding Star of the 21st Century
- Great Man, Who Is a Man of Deeds
- Great Defender
- Savior
- Mastermind of the Revolution
- Highest Incarnation of the Revolutionary Comradeship
- His Excellency
Wikipedia keeps a list. When Kim died in 2011, he was named “General Secretary for Eternity.” According to the state-run Korean Central News Agency, the decision was based on “the unanimous will and desire of all the party members and other people.”
Thorough

Obscure but interesting: In his 1857 history of the West Branch Valley of the Susquehanna River, John Franklin Meginness quotes a 1793 indenture that purports to trace the title to a plot of Pennsylvania land back to the creation of mankind:
Whereas, the Creator of the earth, by parole and livery of seisin, did enfeoff the parents of mankind, to wit, Adam and Eve, of all that certain tract of land, called and known in the planetary system by the name of The Earth, together with all and singular the advantages, woods, waters, water-courses, easements, liberties, privileges, and all others the appurtenances whatsoever thereunto belonging, or in any wise appertaining to have and to hold to them the said Adam and Eve, and the heirs of their bodies lawfully to be begotten, in fee-tail general forever, as by the said feoffment recorded by Moses, in the first chapter of the first book of his records commonly called Genesis, more fully and at large appears on reference being thereunto had …
This goes on for four pages, tracing ownership through the Six Nations of North America to William Penn and finally to one Flavel Roan, the “witty and rather eccentric gentleman” who Meginness says drew up the deed. “His education was good, and his penmanship superior.”
Parting Words
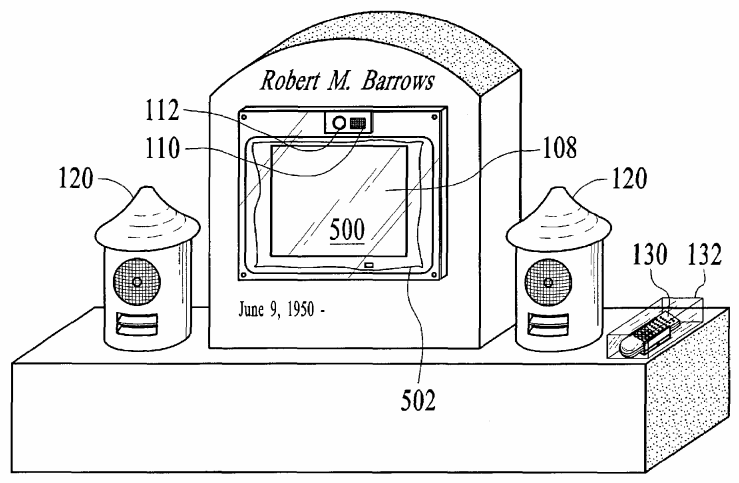
Inventor Robert Barrows thought up a high-tech memorial in 2005: a hollowed-out headstone equipped with a weatherproofed computer monitor.
“I envision being able to walk through a cemetery using a remote control, clicking on graves and what all the people buried there have to say,” he told the Wall Street Journal. “They can say all the things they didn’t have the opportunity or guts to say when they were alive.”
He estimated that a “video-enhanced grave marker” might add $4,000 to the cost of a high-end $4,000 tombstone. If they really take off we’ll need wireless headsets to keep down the racket at the cemetery:
05/09/2017 They’re already doing this in Slovenia. (Thanks, Dan.)
Double Alphamagic Squares
In 1986 British electronics engineer Lee Sallows invented the alphamagic square:
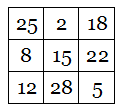
As in an ordinary magic square, each row, column, and long diagonal produces the same sum. But when the number in each cell is replaced by the length of its English name (25 -> TWENTY-FIVE -> 10), a second magic square is produced:
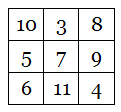
Now British computer scientist Chris Patuzzo, who found the percentage-reckoned pangram that we covered here in November 2015, has created a double alphamagic square:

Each row, column, and long diagonal here totals 303370120164. If the number in each cell is replaced by the letter count of its English name (using “and” after “hundred,” e.g. ONE HUNDRED AND FORTY-EIGHT BILLION SEVEN HUNDRED AND TWENTY-EIGHT MILLION THREE HUNDRED AND SEVENTY-EIGHT THOUSAND THREE HUNDRED AND SEVENTY-EIGHT), then we get a new magic square, with a common sum of 345:
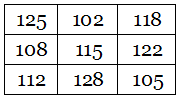
And this is itself an alphamagic square! Replace each number with the length of its name and you get a third magic square, this one with a sum of 60:
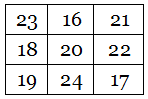
Chris has found 50 distinct doubly alphamagic squares, listed here. I suppose there must be some limit to this — is a triple alphamagic square even possible?
(Thanks, Chris and Lee.)
The Swimming Reindeer

Image: Wikimedia Commons
In 1866 French engineer Peccadeau de l’Isle discovered the sculptures of two swimming reindeer on the banks of the River Aveyron. Each had been carved from a mammoth tusk about 13,000 years ago. The carvings had historic as well as artistic value: They showed that humans, mammoths, and reindeer had coexisted in France during the ice age, when the climate of France resembled that of modern Siberia.
Amazingly, it wasn’t until 1904 that anyone thought to try fitting the two pieces together — it was discovered that they were two parts of a single sculpture. Today they form the oldest piece of art in the British Museum.
