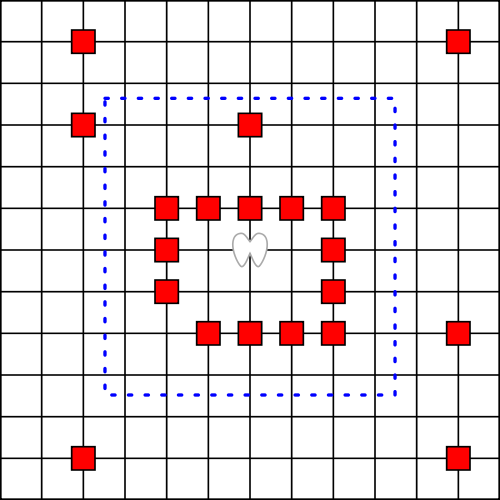
An angel stands on an infinite chessboard. On each turn she can move at most 3 king’s moves from her current position. Play then passes to a devil, who can eat any square on the board. The angel can’t land on an eaten square, but she can fly over it, as angels have wings. (In the diagram above, the angel starts at the origin of the grid and, since she’s limited to 3 king’s moves, can’t pass beyond the blue dotted boundary on her next turn.)
The devil wins if he can strand the angel by surrounding her with a “moat” 3 squares wide. The angel wins if she can continue to move forever. Who will succeed?
John Conway, who posed this question in 1982, offered $100 for a winning strategy for an angel of sufficiently high “power” (3 moves may not be enough; in fact a 1-power angel, an actual chess king, will lose). He also offered $1000 for a strategy that will enable a devil to win against an angel of any power.
It’s not immediately clear what strategy can save the angel. If she simply flees from nearby eaten squares, the devil can build a giant horseshoe and drive her into it. If she sprints in a single direction, the devil can build an impenetrable wall to stop her.
In fact it wasn’t until 2006 that András Máthé and Oddvar Kloster both showed that the angel has a winning strategy. In some variants, in higher dimensions, it’s still not certain she can survive.
(John H. Conway, “The Angel Problem,” in Richard J. Nowakowski, ed., Games of No Chance, 1996.)