
Ukrainian artist Oleg Shuplyak specializes in “Hidden Images,” in which famous faces emerge from simple scenes.
Initially trained as an architect, he’s been a member since 2000 of the National Union of Artists of Ukraine.

Ukrainian artist Oleg Shuplyak specializes in “Hidden Images,” in which famous faces emerge from simple scenes.
Initially trained as an architect, he’s been a member since 2000 of the National Union of Artists of Ukraine.
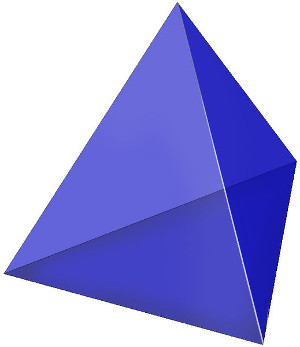
In the humble tetrahedron, each face shares an edge with each other face. Surprisingly, there’s only one other known polyhedron in which this is true — the Szilassi polyhedron, discovered in 1977 by Hungarian mathematician Lajos Szilassi:
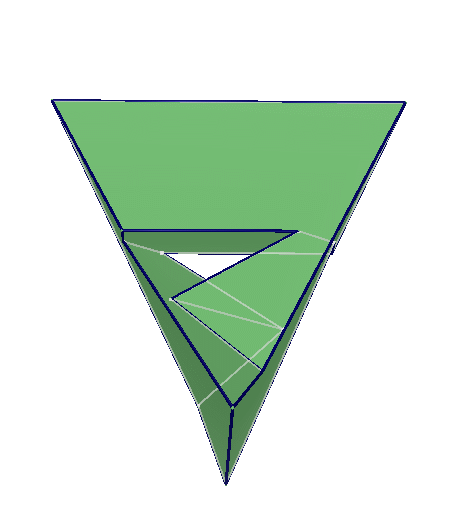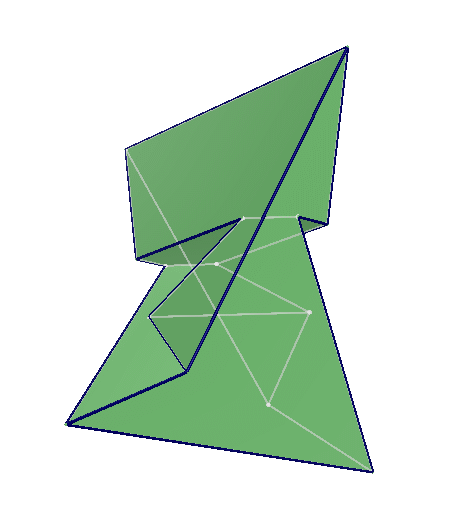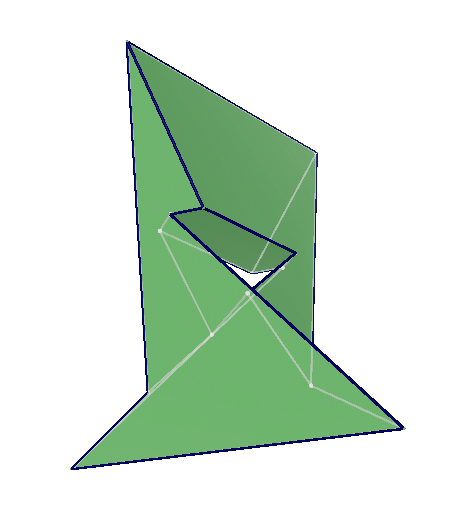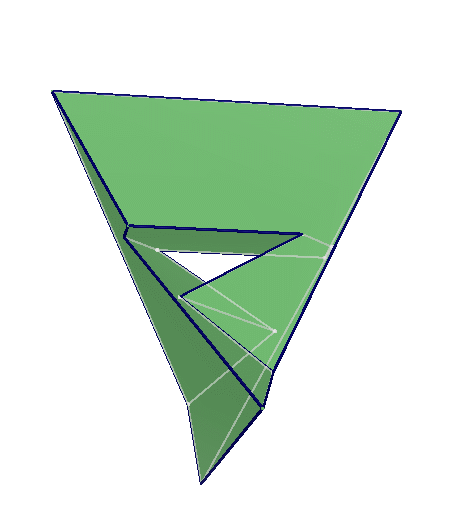
If there’s a third such creature it would have 44 vertices and 66 edges, and no one knows whether such a shape could even be contrived. It remains an unsolved problem.

oppidan
adj. of a university town

The Mercantile Library of Cincinnati has a 10,000-year lease. When Cincinnati College burned in 1845, the young men of the city’s Mercantile Library Association helped to rebuild it. As a reward, the library was given a lease of ten millennia on the 11th and 12th floors of the Mercantile Library Building in downtown Cincinnati.
The current lease will expire in the year 11845 — but it’s renewable.

Linguist Ken Hale had a preternatural ability to learn new languages. “It was as if the linguistic faculty which normally shuts off in human beings at the age of 12 just never shut off in him,” said his MIT colleague Samuel Jay Keyser.
“It’s more like a musical talent than anything else,” Hale told The New York Times in 1997. “When I found out I could speak Navajo at the age of 12, I used to go out every day and sit on a rock and talk Navajo to myself.” Acquiring new languages became a lifelong obsession:
In Spain he learnt Basque; in Ireland he spoke Gaelic so convincingly that an immigration officer asked if he knew English. He apologised to the Dutch for taking a whole week to master their somewhat complex language. He picked up the rudiments of Japanese after watching a Japanese film with subtitles.
He estimated that he could learn the essentials of a new language in 10 or 15 minutes, well enough to make himself understood, if he could talk to a native speaker (he said he could never learn a language in a classroom). He would start with parts of the body, he said, then animals and common objects. Once he’d learned the nouns he could start to make sentences and master sounds, writing everything down.
He devoted much of his time to studying vanishing languages around the world. He labored to revitalize the language of the Wampanoag in New England and visited Nicaragua to train linguists in four indigenous languages. In 2001 his son Ezra delivered his eulogy in Warlpiri, an Australian aboriginal language that his father had raised his sons to speak. “The problem,” Ken once told Philip Khoury, “is that many of the languages I’ve learned are extinct, or close to extinction, and I have no one to speak them with.”
“Ken viewed languages as if they were works of art,” recalled another MIT colleague, Samuel Jay Keyser. “Every person who spoke a language was a curator of a masterpiece.”
Arrange the first n2 odd numbers in a square (here n = 6):
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 51 53 55 57 59 61 63 65 67 69 71
Now, no matter n, the sum of the first row is n2, the sum of either long diagonal is n3, and the sum of the whole array is n4.
(From Edward Barbeau’s Power Play, 1997.)
https://www.youtube.com/watch?v=zc40EPd-MzQ
Buster Keaton’s 1925 silent comedy Seven Chances contains a remarkable transition — Keaton gets into a car and the setting dissolves into his destination. The car never moves. In 1964 interviewer Kevin Brownlow asked how this was done:
KEATON: Now that automobile’s got to be exactly the same distance, the same height and everything, to make that work, because the scene overlaps but I don’t.
BROWNLOW: Now, what about lighting on it?
KEATON: Standard lighting.
BROWNLOW: It was interior.
KEATON: No, all exterior.
BROWNLOW: If it was standard lighting and the sun wasn’t in the right place, the shadows would …
KEATON: We made sure of that, same time of day so the shadows would [be in the same place]. But for that baby, we used surveying instruments, so that the front part of the car would be the same distance from [the camera], the whole shooting match.
Keaton was also rumored to have relied on surveyors’ tools in 1924’s Sherlock Jr., but he said it wasn’t so. “Every cameraman in the picture business went and saw that picture more than once, trying to figure out how in hell we did some of that. Oh, there were some great shots in that baby!”
(From Kevin W. Sweeney, ed., Buster Keaton Interviews, 2007.)
In 2006, screenwriter Gregory K. Pincus invited the readers of his blog to submit “Fibs,” poems of six lines whose syllable counts reflect the Fibonacci sequence:
One
Small,
Precise,
Poetic,
Spiraling mixture:
Math plus poetry yields the Fib.
Predictably, this took off on Slashdot, where it spawned a thousand variations:
01 It
01 is
02 really
03 not taxing
05 to create a Fib,
08 but still they are interesting
13 sequences of numbers. We are familiar with
21 the ‘rabbit generation’ origins of the sequence, but it can also describe
34 the number of petals on a flower, or the number of curves on a sunflower head, on a pineapple, or even on a pinecone.
And from there it expanded around the world. “The success of this story was entirely because the poem was based on the Fibonacci sequence,” Slashdot founder Rob Malda told the Poetry Foundation. “Geeks love interesting number sequences, and that one is way up there. Generally speaking literature by itself isn’t our typical subject matter, but interesting use of math definitely is.”
“To my surprise (and joy), I continue to find new threads of Fibs popping up all around the Web,” wrote Pincus, who eventually parlayed the idea into a novel. “I’ve seen Fibs in over a dozen different languages, and I’d also note that today a cat left a post in the comments of The Fib, joining a priorly poetic dog, so I think it’s safe to say that Fibs travel well.”
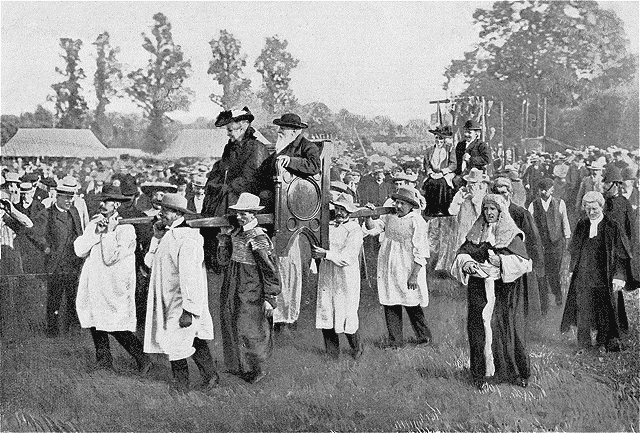
The Essex market town of Great Dunmow keeps alive a curious tradition: It awards a flitch of bacon to any married couple who can swear after a year and a day that they have not regretted their marriage. The custom goes back to the 13th century and perhaps even earlier; Chaucer mentions it as a well-established tradition. A similar ceremony used to be held at Wychnoure — two neighbors had to hear this oath and agree it was true:
Hear ye, Sir Philip de Somervile, lord of Whichenoure, maintainer and giver of this Bacon, that I, (husband), syth I wedded (wife), my wyfe, and syth I had her in my kepyng and at wylle, by a Yere and a Day after our Marryage, I would not have changed for none other, farer ne fowler, richer ne powrer, ne for none other descended of gretter lynage, sleeping ne waking, at noo time; and if the said (wife) were sole, and I sole, I would take her to be my wyfe before all the wymen of the worlde, of what condytions soevere they be, good or evyle, as helpe me God, and his Seyntys, and this flesh, and all fleshes.
Sadly, almost no one gets the bacon. Horace Walpole noted in 1760 that the Whichnoure flitch had not been claimed in 30 years, and records show that between 1444 and 1751 only six couples managed to win the Dunmow flitch.
But it’s not too late to try. The tradition had nearly died out when novelist William Harrison Ainsworth revived it with The Flitch of Bacon in 1854, and Dunmow has kept it alive since then. The modern trials are held each leap year, so the next one is in 2020. You’ll be cross-examined, and the case will be decided by a jury. But win or lose you get to visit Dunmow. As Walpole wrote, “If you love a prospect, or bacon, you will certainly come hither.”

In Circularity, Ron Aharoni mentions a story by Raymond Smullyan. On a certain island there are two kinds of people, those who always lie and those who always tell the truth. One day an islander is arrested on suspicion of murder. At his trial he says, “The murderer is a liar.”
Smullyan argues that this piece of evidence alone should acquit him. If the man is honest, then what he says is true, the murderer is a liar, and since he himself is a truth-teller he cannot be the guilty party. On the other hand, if he’s a liar then his testimony is false, which means that the murderer is in fact not a liar, and once again he cannot be guilty. Either way, he proves his innocence by showing that the murderer and himself belong to two different tribes.
Aharoni adds, “The problem is that the man was found beside the corpse with a bloody knife in his hand and a wide smile on his face. He is obviously the murderer, which means that he managed to prove an obvious fallacy. It seems that using his method, he can prove anything. And indeed he can. See what he is claiming when stating that the murderer is a liar: ‘If I am the murderer, then I am a liar’, which means ‘if I am the murderer then this is a lie’. In other words — ‘If I am the murderer then L is true’. And … this proves that ‘I am not the murderer.'”