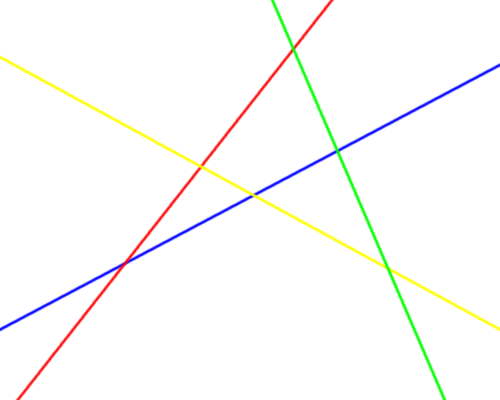
Four straight roads cross a plain. No two are parallel, and no three meet in a point. On each road is a traveler who moves at some constant speed. If Blue and Red meet each other at their crossroad, and each of them meets Yellow and Green at their respective crossroads, will Yellow and Green necessarily meet at their own crossroad?
Suprisingly, the answer is yes. Rob Fatland offers a beautiful solution at the CTK Exchange:
Imagine the whole scenario unfolding from Blue’s rest frame; that is, regard Blue as unmoving and consider the movements of the other travelers relative to him. What does he see? Objectively we know that each traveler moves along a straight line at a constant speed, eventually encounters Blue, and moves on, so from Blue’s perspective each of them moves directly toward him on a straight line, passes through his position, and continues.
Very well, let Red do that. But we know that Red also encounters Yellow and Green without deviating from his own path. And we know that (from Blue’s perspective) Yellow and Green are also traveling straight lines that intersect Blue’s position. This can only mean that Red, Yellow, and Green are all traveling along the same straight line from Blue’s point of view. And this means that Yellow and Green must meet one another.
(It might be objected that two points traveling the same line needn’t meet if they’re going in the same direction at the same speed. But here this would mean that two of the roads are parallel, and that possibility is excluded by the conditions of the problem.)
05/27/2016 UPDATE: Reader Derek Christie recalls a three-dimensional solution: “Make a time axis perpendicular to the plane. Then each traveller moves in a straight line trajectory through this 3D space. Blue and Red meet at a particular place and time, so their two trajectories must meet at a point, and these two trajectories define a plane. Both Yellow and Green trajectories meet the Blue and Red trajectories and so also lie in this same plane. So Yellow and Green must also meet somewhere in that plane.”