
Here are five new lateral thinking puzzles to test your wits and stump your friends — play along with us as we try to untangle some perplexing situations using yes-or-no questions.

Here are five new lateral thinking puzzles to test your wits and stump your friends — play along with us as we try to untangle some perplexing situations using yes-or-no questions.

There’s a statue of Lenin in Seattle. Originally sculpted by Bulgarian artist Emil Venkov, it was installed in Poprad, Czechoslovakia, in 1988, just a year before the Velvet Revolution. Visiting American English teacher Lewis Carpenter found it lying in a scrapyard waiting to be melted down; he offered $13,000 for it and shipped it home to Issaquah, Washington.
When Carpenter died in an auto accident, the statue found its way to Seattle’s Fremont neighborhood, where the local chamber of commerce has agreed to hold it in trust until a buyer can be found. The current asking price is $250,000.
For now the founder of the League of Struggle for the Emancipation of the Working Class stands at the intersection of Fremont Place North, North 36th Street, and Evanston Avenue North, where he is regularly decorated with Christmas lights. Six-year-old Colin Sackett told the Seattle Post-Intelligencer, “It just makes me remember Christmas is coming. And it makes me remember Hanukkah, too.”
There was an old man who said, “Do
Tell me how I’m to add two and two!
I’m not very sure
That it does not make four,
But I fear that is almost too few.”
A mathematician confided
A Möbius strip is one-sided.
You’ll get quite a laugh
If you cut one in half,
For it stays in one piece when divided.
A mathematician named Ben
Could only count modulo ten.
He said, “When I go
Past my last little toe,
I have to start over again.”
By Harvey L. Carter:
‘Tis a favorite project of mine
A new value of π to assign.
I would fix it at 3,
For it’s simpler, you see,
Than 3.14159.
J.A. Lindon points out that 1264853971.2758463 is a limerick:
One thousand two hundred and sixty
four million eight hundred and fifty
three thousand nine hun-
dred and seventy one
point two seven five eight four six three.
From Dave Morice, in the November 2004 Word Ways:
A one and a one and a one
And a one and a one and a one
And a one and a one
And a one and a one
Equal ten. That’s how adding is done.
(From Through the Looking-Glass:)
‘And you do Addition?’ the White Queen asked. ‘What’s one and one and one and one and one and one and one and one and one and one?’
‘I don’t know,’ said Alice. ‘I lost count.’
‘She can’t do Addition,’ the Red Queen interrupted.
An anonymous classic:
The integral z-squared dz
From one to the cube root of three
Times the cosine
Of three pi over nine
Equals log of the cube root of e.
A classic by Leigh Mercer:
A dozen, a gross, and a score
Plus three times the square root of four
Divided by seven
Plus five times eleven
Is nine squared and not a bit more.
UPDATE: Reader Jochen Voss found this on a blackboard at Warwick University:
If M’s a complete metric space
(and non-empty), it’s always the case:
If f’s a contraction
Then, under its action,
Exactly one point stays in place.
And Trevor Hawkes sent this:
A mathematician called Klein
Thought the Möbius strip was divine.
He said if you glue
The edges of two
You get a nice bottle like mine.
Many thanks to reader Colin White for this:
In her 2005 song “π,” Kate Bush sings the number π to its 78th decimal place, then jumps abruptly to the 101st and finishes at the 137th.
The BBC’s More or Less advanced the “Kate Bush conjecture”: that the digits that Bush sings are contained somewhere in the decimal expansion of π — just not at the start.
The conjecture is true if π turns out to be a “normal” number, meaning essentially that all possible sequences of digits (of a given length) appear equally often in its expansion.
π hasn’t been proven to have this property, though it’s expected to be the case. So, for now, “The Kate Bush conjecture is plausible but unproven.”

For the writer of fantastic stories to help the reader to play the game properly, he must help him in every possible unobtrusive way to domesticate the impossible hypothesis. He must trick him into an unwary concession to some plausible assumption and get on with his story while the illusion holds. And that is where there was a certain slight novelty in my stories when first they appeared. Hitherto, except in exploration fantasies, the fantastic element was brought in by magic. Frankenstein even, used some jiggery-pokery magic to animate his artificial monster. There was trouble about the thing’s soul. But by the end of last century it had become difficult to squeeze even a momentary belief out of magic any longer. It occurred to me that instead of the usual interview with the devil or a magician, an ingenious use of scientific patter might with advantage be substituted. That was no great discovery. I simply brought the fetish stuff up to date, and made it as near actual theory as possible.
— H.G. Wells, June 1934 (from the H.G. Wells Scrapbook)
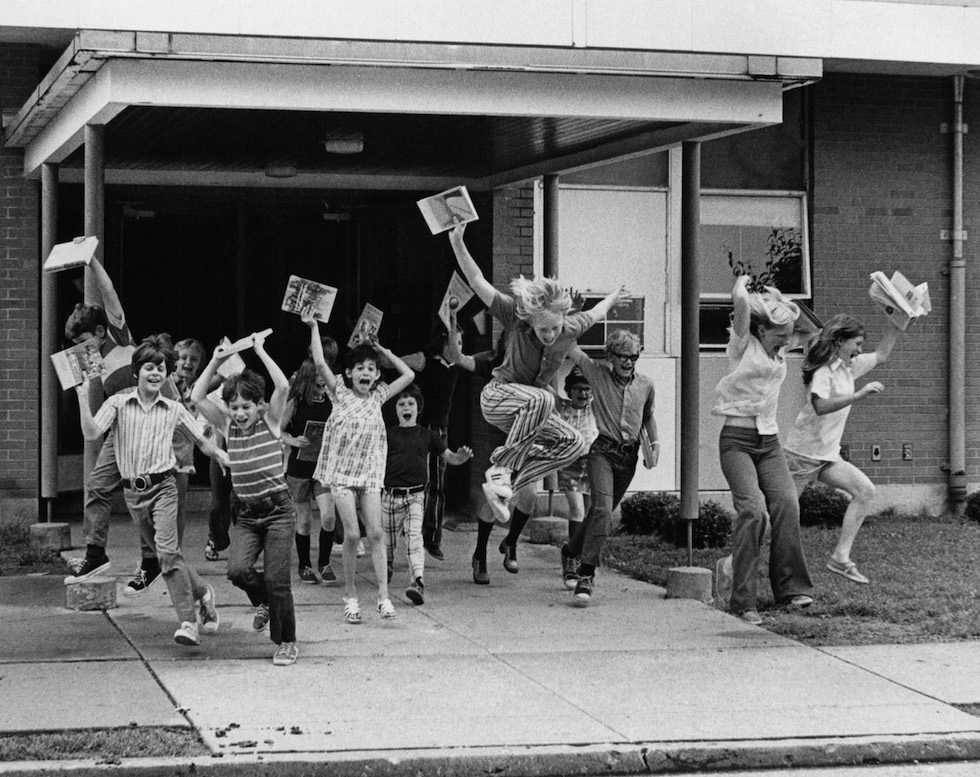
School’s out for summer, Belleville, Illinois, 1974.
“There is, on the whole, nothing on earth intended for innocent people so horrible as a school.” — George Bernard Shaw
“It is a very grave mistake to think that the enjoyment of seeing and searching can be promoted by means of coercion and a sense of duty.” — Albert Einstein
“I have not the least doubt that school developed in me nothing but what was evil and left the good untouched.” — Edvard Grieg
“I hope we still have some bright twelve-year-olds who are interested in science. We must be careful not to discourage our twelve-year-olds by making them waste the best years of their lives on preparing for examinations.” — Freeman Dyson
“Education has become one of the chief obstacles to intelligence and freedom of thought.” — Bertrand Russell
“Spoon feeding in the long run teaches us nothing but the shape of the spoon.” — E.M. Forster

During the burning of Washington in the War of 1812, when a British expeditionary force leveled a cannon at the Patent Office, superintendent William Thornton “put himself before the gun, and in a frenzy of excitement exclaimed: ‘Are you Englishmen or only Goths and Vandals? This is the Patent Office, a depository of the ingenuity of the American nation, in which the whole civilized world is interested. Would you destroy it? If so, fire away, and let the charge pass through my body.'”
“The effect is said to have been magical upon the soldiers, and to have saved the Patent Office from destruction. … When the smoke cleared from the dreadful attack, the Patent Office was the only Government building … left untouched.”
(From R. Beresford’s Brief History of the United States Patent Office From Its Foundation, 1886.)

No women are allowed on Greece’s Mount Athos, the site of 20 Eastern Orthodox monasteries, because they would hinder the monks’ progress toward spiritual enlightenment. Mary alone represents her sex on the mountain.
The ban has been in place since an imperial decree in 1046, with a few colorful exceptions:
The rule extends even to hens, cows, nanny-goats, and sows, which means that dairy products and eggs have to be brought in from outside. Female cats, insects, and songbirds are admitted.
In 2003 the European Parliament passed a resolution saying the ban violated “the universally recognised principle of gender equality,” but it remains in place — even female sightseers must stay at least 500 meters offshore.
Here are the proper prime divisors of the first nine natural numbers (a proper prime divisor is a prime different from n that divides n evenly):
1: (none)
2: (none)
3: (none)
4: 2 × 2
5: (none)
6: 2 × 3
7: (none)
8: 2 × 2 × 2
9: 3 × 3
So, if we include repeated instances of a given factor:
Mathematicians Ana Luzón and Manuel A. Morón of Universidad Politecnica de Madrid point out a coincidence: The numerals in each of these groups have the same basic shape — within each group it’s possible to transform one numeral into another by bending, shrinking, and expanding. So, for example, it’s possible to bend a numeral 1 made of clay into a 2 or a 7, but not into a 9 — we’re not allowed to poke a new hole in the clay or to affix one part of it to another.
Luzón and Morón write that if two of these nine numerals have the same number of proper prime divisors, then those two will “cut a sheet in the same number of pieces if you write them down with a scalpel.” And if the scalpel doesn’t cut the sheet into multiple pieces, then the number you’re writing is prime (except for 1).
Note: This works only if the numeral 4 is “closed” at the top, not open. So this post will make sense if you’re reading it on Futility Closet (which uses the “closed” font Georgia), but possibly not if you’re reading it in a different font elsewhere. Maybe this tells us how 4 “ought” to be written!
(Ana Luzón and Manuel A. Morón, “4 or 4? Mathematics or Accident?” Mathematics Magazine 75:4 [October 2002], 274.)
Order a beer at Kayabukiya Tavern, in Japan’s Tochigi prefecture, and it will be brought to you by one of five monkeys. Owner Kaoru Otsuka started his business nearly 30 years ago, but business really took off when he brought his pet macaque to the premises and got it to hand a wet oshibori towel to a customer. Now the monkeys hand out oshibori and beer and perform on a makeshift stage.
Under animal welfare laws the monkeys work only two hours a day, and customers give them boiled soya beans as tips for their service. Now they’ve begun donning human masks and wigs — perhaps they’ll soon be opening a restaurant of their own: