
By T.R. Dawson. “The problem is for each White man to capture the corresponding Black man in such a way that the routes traversed by each man never come in contact with one another.”

By T.R. Dawson. “The problem is for each White man to capture the corresponding Black man in such a way that the routes traversed by each man never come in contact with one another.”

In the contentious presidential election of 1876, the campaign of Democrat Samuel Tilden sent many enciphered messages to its agents in contested states. Two years after the election, the New York Daily Tribune published some of the deciphered telegrams, showing that Tilden’s campaign had tried to bribe election officials to win the race. Here’s one of the telegrams:

Since only 10 letters are used, it seems likely that the cipher refers to pairs of letters. So if each successive pair in the message is assigned to an arbitrary letter:
![]()
… then we have a simple cryptogram that can be solved to give the message:

Tilden’s campaign did the same thing with pairs of numbers. For example, this message:
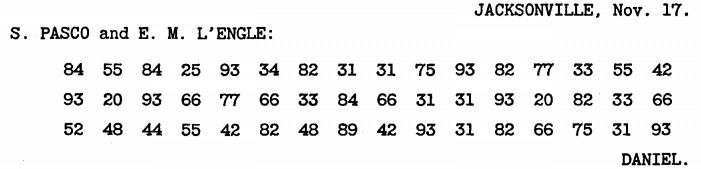
… turns out to mean:

In 1879 the Tribune’s experts worked out the letter and number pairs that had corresponded to each letter of the alphabet:

But it wasn’t until 1952 that cryptographer William F. Friedman reconstructed the table that the agents had used to remember this system:
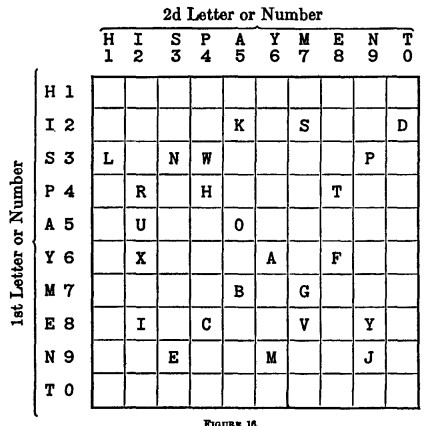
“It is amusing to note that the conspirators selected as their key a phrase quite in keeping with their attempted illegalities — HIS PAYMENT — for bribery seems to have played a considerable part in that campaign.”
(From Beaird Glover, Secret Ciphers of the 1876 Presidential Election, 1991.)

Guy Gabaldon was an untested Marine when he landed on the Pacific island of Saipan during World War II. But he decided to fight the war on his own terms, venturing alone into enemy territory and trying to convince Japanese soldiers to surrender voluntarily. In this week’s episode of the Futility Closet podcast we’ll follow Gabaldon’s dangerous crusade and learn its surprising results.
We’ll also examine Wonder Woman’s erotic origins and puzzle over an elusive murderer.
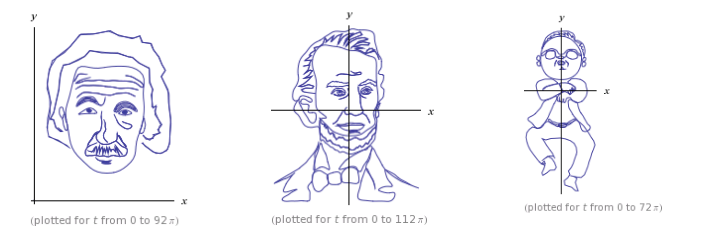
Wolfram Alpha has a collection of parametric curves that produce portraits of famous people — above are Albert Einstein, Abraham Lincoln, and PSY.
Wolfram chief scientist Michael Trott explains how it’s done in three blog posts.
(Thanks, Danesh.)

During the Great Depression, Texas carpenter Ernesto Guerrero could not find work, and his family received boxes of food through Franklin Roosevelt’s New Deal assistance program. To show her appreciation, Ernesto’s daughter Ernestine spent a year developing her skills with a coping saw and another year carving this fretwork clock case from the leftover grocery boxes.
She sent it to Roosevelt in 1937. “This is the best I have ever done in my life,” she wrote. “I know that you have many pretty things, but please accept and keep this piece of work from a poor girl that doesn’t have anything, also to show you how much we admire you … as a man of great ideals and a big heart toward humanity.”
FDR put the case on display, first at his family estate in Hyde Park, N.Y., and later as part of the Franklin D. Roosevelt Library Museum Collection — the first presidential library.
(From Robert Cohen, Dear Mrs. Roosevelt: Letters from Children of the Great Depression, 2003.)

In 1953, 150 golfers participated in a “Golden Ball” competition in which they teed off at the first tee at Cill Dara Golf Club in Kildare, Ireland, and holed out at the 18th hole at the Curragh, about 5 miles away. A prize of £1 million was offered for a hole in one, which would have been well earned, as the distance is 8,800 yards.
In The Book of Irish Golf, John Redmond writes, “The hazards to be negotiated included the main Dublin-Cork railway line and road, the Curragh racecourse, Irish army tank ranges and about 150 telephone lines.” The trophy went to renowned long hitter Joe Carr, who covered the distance in 52 shots.
In 1920, Rupert Lewis and W. Raymond Thomas played over 20 miles of countryside from Radyr Golf Club near Cardiff, Wales, to Southerndown Golf Club at Ewenny, near Bridgend. Most onlookers guessed that they’d need at least 1,000 strokes, but they completed the journey in 608, playing alternate strokes. “At one time, the pair had to wade knee deep to ford a river,” writes Jonathan Rice in Curiosities of Golf, “but dried out by jumping a hedge while being chased by a bull.”
Inspired by the P.G. Wodehouse story “The Long Hole,” eight members of the Barnet Rugby Hackers Golf Club played 23 miles across Ayrshire in 1968, from Prestwick, the site of the first Open Championship, to Turnberry, the site of that year’s event. They lost “only” 50 or 60 balls while negotiating “a holiday camp, a dockyard, a stately home, a croquet lawn, several roofs, the River Doon,” and another bull, for a final score of 375 to 385.
N.T.P. Murphy gives a few more in A Wodehouse Handbook: In 1913 two golfers played 26 miles from Linton Park near Maidstone to Littleston-on-Sea in 1,087 strokes; Doe Graham played literally across country in 1927, from Florida’s Mobile Golf Club to Hollywood, a distance of 6,160,000 yards (I don’t have the final score, but he’d taken 20,000 strokes by the time he reached Beaumont, Texas); and Floyd Rood played from the Atlantic to the Pacific in 1963 in 114,737 shots.
The object of golf, observed Punch in 1892, “is to put a very small ball into a very tiny and remotely distant hole, with engines singularly ill adapted for the purpose.”
03/25/2017 UPDATE: Reader Shane Bennett notes that Australia’s Nullarbor Links claims to be the world’s longest golf course — players drive from Ceduna in South Australia to Kalgoorlie in Western Australia, stopping periodically to play a hole. Par for the 18 holes is only 73, but the course stretches over 1,365 kilometers. (Thanks, Shane.)

“Dirt is not dirt, but only matter in the wrong place.” — Lord Palmerston

For four months in 1840 Edgar Allan Poe conducted a puzzle column for the Philadelphia newspaper Alexander’s Daily Messenger. In that time he defied his readers to send him a cryptogram that he could not solve, and at the end of his tenure he declared himself undefeated. One of the later challenges came from 17-year-old Schuyler Colfax of New Carlisle, Iowa, who would grow up to become vice president of the United States:
Dear Sir — As you have in your Weekly Messenger defied the world to puzzle you by substituting arbitrary signs, figures, etc. for the different letters of the alphabet, I have resolved to try my utmost to corner you and your system together, and have manufactured the two odd looking subjects which accompany this as avant couriers. … If you succeed in solving the accompanying, I will, of course, as you request, acknowledge it publicly to my friends.
Poe responded: “We have only time, this week, to look at the first and longest cypher — the unriddling of which, however, will no doubt fully satisfy Mr. Colfax that we have not been playing possum with our readers.” Here’s Colfax’s cryptogram:
8n()58†d w!0 b† !x6n†z k65 !nz k65,8l†n b)x 8nd)Pxd !zw8x 6k n6 36w-†nd!x86n;
x=†0 z†,5!z† x=† w8nz 8n 8xd 62n †dx††w !nz k653† 8x x6 5†36l†5 8xd P†l†P b0 5†l†n,†.
()n8)d
What’s the solution?
It’s well known that the sum of the cubes of the first n integers equals the square of their sum:
13 + 23 + 33 + 43 + 53 = (1 + 2 + 3 + 4 + 5)2
California State University mathematician David Pagni found another case in which the sum of cubes equals the square of a sum. Take any whole number:
28
List all its divisors:
1, 2, 4, 7, 14, 28
Count the number of divisors of each of these:
1 has 1 divisor
2 has 2 divisors
4 has 3 divisors
7 has 2 divisors
14 has 4 divisors
28 has 6 divisors
Now cube these numbers and sum the cubes:
13 + 23 + 33 + 23 + 43 + 63 = 324
And sum the same set of numbers and square the sum:
(1 + 2 + 3 + 2 + 4 + 6)2 = 324
The two results are the same: The sum of the cubes of these numbers will always equal the square of their sum.
(David Pagni, “An Interesting Number Fact,” Mathematical Gazette 82:494 [July 1998], 271-273.)
03/10/2017 UPDATE: Reader Kurt Bachtold points out that this was originally discovered by Joseph Liouville, a fact that I should have recalled, as I’d written about it in 2011. (Thanks, Kurt.)

In 1818 caricaturist George Cruikshank saw several people hanging from a gibbet near Newgate Prison in London and learned to his horror that they had been executed for passing forged one-pound notes — at the time, doing so even unknowingly was punishable by death or transportation.
The fact that a poor woman could be put to death for such a minor offence had a great effect upon me — and I at that moment determined, if possible, to put a stop to this shocking destruction of life for merely obtaining a few shillings by fraud; and well knowing the habits of the low class of society in London, I felt quite sure that in very many cases the rascals who forged the notes induced these poor ignorant women to go into the gin-shops to ‘get something to drink,’ and thus pass the notes, and hand them the change.
He went home and dashed off this sketch, which was then printed on the post paper used by the bank, so that it would resemble counterfeit currency. “The general effect was of a counterfeit, but closer examination revealed that every element of the official design had been replaced by a savage parody,” writes Robert L. Patten in George Cruikshank’s Life, Times, and Art. The seal shows Britannia eating her children, the stamp depicts 12 tiny heads in prison, and the pound sign is a coiled hangman’s rope.
The protest created a sensation, and remedial legislation was passed. Cruikshank’s satire, noted the Examiner, “ought to make the hearts of the Bank Directors ache at the sight.”