
Asteroid 46610 was named Bésixdouze in homage to Antoine de Saint-Exupéry’s character Le Petit Prince, who lived on Asteroid B-612.
B-612 is 46610 in hexadecimal.
(Thanks, Dan.)

Asteroid 46610 was named Bésixdouze in homage to Antoine de Saint-Exupéry’s character Le Petit Prince, who lived on Asteroid B-612.
B-612 is 46610 in hexadecimal.
(Thanks, Dan.)
In the 1950s a passenger rail line served Ithaca, N.Y. It was the only reliable way to get to Ithaca, working in all seasons and weather conditions, but it was slow and uncomfortable, so when possible many people traveled instead by car, air, or bus. The railway didn’t make enough revenue to continue the service, and in May 1959 it shut down the line.
The commuters expressed real dismay. Their daily choices to travel by other means had been too “small” to reflect their desire for continued rail service; the railway, by contrast, had had to make one big, long-term decision whether to maintain the line. Both sides were acting rationally, but they’d reached an outcome that no one preferred.
Cornell economist Alfred E. Kahn called this the “tyranny of small decisions”:
The short- and long-run determinations by business men are governed by decisions of customers involving a corresponding range in size and time-perspective — to buy a single candy bar, a camping trip, an automobile, a house, or to enter a rental contract of short or long duration. Still, the ‘size’ or importance of the individual choices by customers is typically less than of those made by the business man, so that each of the latter’s decisions reflects a prospective adding up of the consequences of a large number of customer actions taking place over a period of time.
And the “sum” of these small decisions may not reflect what people really want. “[I]f one hundred consumers choose option x, and this causes the market to make decision X (where X equals 100x), it is not necessarily true that those same consumers would have voted for that outcome if that large decision had ever been presented for their explicit consideration. If this is true, the consumer can be victimized by the narrowness of the contexts in which he exercises his sovereignty.”
(Alfred E. Kahn, “The Tyranny of Small Decisions: Market Failures, Imperfections, and the Limits of Economics,” Kvklos 19:1 [1966], 23-47.)

During World War II, as they mulled whether to attempt an invasion of the continent, the Allies needed to estimate the number of tanks Germany was producing. They asked their intelligence services to guess the number by spying on German factories and counting tanks on the battlefield, but these efforts produced contradictory estimates. Finally they resorted to statistical analysis.
They did this by studying the serial numbers on captured and destroyed German tanks. Suppose German tanks are numbered sequentially 1, 2, 3, …, B, where B is the total number of tanks that we seek to know. And suppose that we have five captured tanks whose serial numbers are 21, 35, 42, 60, and 89. It turns out that
where N is the sample size (here, 5) and M is the highest sampled number (here, 89). In this example, the formula tells us that B = 105.8, so we’d estimate that 106 tanks had been produced at that time.
In the event, Allied statisticians reportedly estimated that the Germans had produced 246 tanks per month between June 1940 and September 1942. Intelligence estimates had put the total at about 1,400. When the Allies captured German production records after the war, they found that they had produced 245 tanks per month during those three years, almost precisely what the statisticians had predicted, and less than 20 percent of the intelligence estimate.
(Thanks, Ryan.)

In 1777, in conversation with diplomat Arthur Lee, Benjamin Franklin reflected on the “miracle” of the American Revolution:
To comprehend it we must view a whole people for some months without any laws or government at all. In this state their civil governments were to be formed, an army and navy were to be provided by those who had neither a ship of war, a company of soldiers, nor magazines, arms, artillery or ammunition. Alliances were to be formed, for they had none. All this was to be done, not at leisure nor in a time of tranquillity and communication with other nations, but in the face of a most formidable invasion, by the most powerful nation, fully provided with armies, fleets, and all the instruments of destruction, powerfully allied and aided, the commerce with other nations in a great measure stopped up, and every power from whom they could expect to procure arms, artillery, and ammunition, having by the influence of their enemies forbade their subjects to supply them on any pretence whatever. Nor was this all; they had internal opposition to encounter, which alone would seem sufficient to have frustrated all their efforts. … It was, however, formed and established in despite of all these obstacles, with an expedition, energy, wisdom, and success of which most certainly the whole history of human affairs has not, hitherto, given an example.
“He told me the manner in which the whole of this business had been conducted, was such a miracle in human affairs, that if he had not been in the midst of it, and seen all the movements, he could not have comprehended how it was effected.”
(From Lee’s journal, Oct. 25, 1777.)

In 1964, Swedish journalist Åke Axelsson paid a zookeeper to give a brush and paint to a 4-year-old chimpanzee named Peter. Then he chose the best of Peter’s paintings and exhibited them at the Gallerie Christinae in Göteborg, saying they were the work of a previously unknown French artist named Pierre Brassau.
Critic Rolf Anderberg of the Göteborgs-Posten wrote, “Brassau paints with powerful strokes, but also with clear determination. His brush strokes twist with furious fastidiousness. Pierre is an artist who performs with the delicacy of a ballet dancer.”
After Axelsson revealed the hoax, Anderberg maintained that Peter’s work was “still the best painting in the exhibition.”
In one oft-repeated anecdote from the memoirs of Melville Stone, publisher of the Chicago Daily News in the 1870s, the News suspected that the Chicago Post and Mail, published by the McMullen brothers, was pirating its stories. The News retaliated by printing an account of a famine in Serbia, in which the local mayor was quoted as saying (ostensibly in Serbian) ‘Er us siht la Etsll iws nel lum cmeht.’ When the afternoon edition of the Post and Mail duly reproduced the quote, Stone ran to all the other Chicago papers to reveal the hoax: read backward, the supposed quote said ‘The McMullens will steal this sure.’ According to Stone, the Post and Mail never recovered from the embarrassment, and the Daily News was able to buy it for a pittance less than two years later.
— Stuart Banner, American Property: A History of How, Why, and What We Own, 2011
(Thanks, Keith.)

Early one morning in 1912, the residents of Villisca, Iowa, discovered a horrible scene: An entire family had been brutally murdered in their sleep. In this week’s episode of the Futility Closet podcast we’ll describe the gruesome crime, which has baffled investigators for a hundred years.
We’ll also follow the further adventures of German sea ace Felix von Luckner and puzzle over some fickle bodyguards.
It’s said that when Frederick the Great hosted Voltaire at Sanssouci Palace, he sent him this puzzling note:
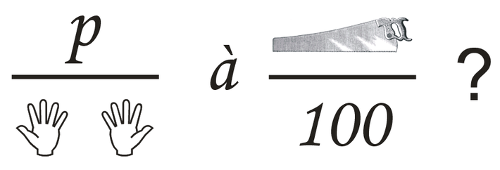
It’s a rebus in French: deux mains sous Pé à cent sous scie? (“two hands under ‘p’ at hundred under saw”) means demain souper à Sanssouci? (“supper tomorrow at Sanssouci?”).
Voltaire replied “Ga!”: Gé grand, A petit! (“big ‘G’, small ‘a’!”) means j’ai grand appétit!, or “I am very hungry!”

More chess masters reside in New York City than in the rest of the United States combined. We’re planning a chess tournament that all American masters are expected to attend, and we want to minimize the total intercity traveling done by the players. The New York players argue that, by this criterion, the tournament should be held in their city. The West Coast players argue that a city should be chosen near the center of the gravity of the players. Where should we hold the tournament?

There are no known pictures of two American presidents’ wives: Martha Jefferson and Margaret Taylor.
We have one silhouette (left) of Jefferson, who was a little over 5 feet tall and had auburn hair and hazel eyes.
And one 1903 book contains a suggested likeness of Taylor (right), who was described during her life as “a fat, motherly looking woman,” “countenance rather stern but it may be the consequence of military association.”
But no portrait of either woman is known to exist. Some artists have attempted renderings based on pictures of their daughters, whom they were said to resemble, but that’s the best we can do.