Podcast Episode 111: Japanese Fire Balloons

Toward the end of World War II, Japan launched a strange new attack on the United States: thousands of paper balloons that would sail 5,000 miles to drop bombs on the American mainland. In this week’s episode of the Futility Closet podcast, we’ll tell the curious story of the Japanese fire balloons, the world’s first intercontinental weapon.
We’ll also discuss how to tell time by cannon and puzzle over how to find a lost tortoise.
Talking

Excerpt of a letter from British general Philip Howele to his wife, Sept. 15, 1915:
It is VILE that all my time should be devoted to killing Germans whom I don’t in the least want to kill. If all Germany could be united in one man and he and I could be shut up together just to talk things out, we could settle the war, I feel, in less than one hour. The ideal war would include long and frequent armistices during which both sides could walk across the trenches and discuss their respective points of view. We are really only fighting just because we are all so ignorant and stupid. And if diplomats were really clever such a thing as war could never be. Shall I desert and see if any of them will listen on the other side? My little German officer was rather flabbergasted when the first question I asked him the other morning, when the escort had gone out and shut the door, and after I’d put him in a comfortable chair and given him a cigarette, was, ‘Now first of all do you really hate me, and if so why?’ He said he didn’t. But then later, when I asked him what we could possibly do to stop all this nonsense, he had no suggestions to make. ‘I have my ideas’ he said but somehow couldn’t express them.
Goodnight … and bless you.
P.
Application

Victor Hugo wrote The Hunchback of Notre-Dame under enormous financial pressure, leaving his table only to eat or sleep.
Finally, his daughter Adèle wrote, “On 14 January, [Notre-Dame] was finished. The bottle of ink that M. Victor Hugo had bought the first day was finished also; he had arrived in the same moment at the last line and at the last drop.
“This gave him, in that moment, the idea of changing his title and calling his novel: What There Is in a Bottle of Ink.”
Progress

What Did George the Third Know?
He never saw a match.
He never saw a bicycle.
He never saw an oil stove.
He never saw an ironclad.
He never saw a steamboat.
He never saw a gas engine.
He never saw a type-writer.
He never saw a phonograph.
He never saw a steel plough.
He never took laughing gas.
He never rode on a tram car.
He never saw a fountain pen.
He never saw a railway train.
He never knew of Evolution.
He never saw a postage stamp.
He never saw a pneumatic tube.
He never saw an electric railway.
He never saw a reaping machine.
He never saw a set of artificial teeth.
He never saw a telegraph instrument.
He never heard the roar of a Krupp gun.
He never saw a threshing machine, but used a flail.
He never saw a pretty girl work on a sewing machine.
He never saw a percussion cap, nor a repeating rifle.
His grandmother did his mending with a darning needle.
He never listened to Edison’s mocking machine or phonograph.
When he went to a hotel he walked upstairs, for they had no lifts.
He never saw a steel pen, but did all his writing with a quill.
He never held his ear to a telephone, or talked to his wife a hundred miles away.
He never saw a fire engine, but when he went to a fire, he stood in line and passed buckets.
He never knew the pleasure and profit to be derived from reading Science Siftings.
— Science Siftings, 1894
Fore!
Temporary rules adopted by London’s Richmond Golf Club during the Battle of Britain:

I had my doubts about this, but the rules are acknowledged by the club itself. While we’re at it: In A Wodehouse Handbook, N.T.P. Murphy notes two unusual tournament rules at the annual Bering Sea Ice Classic in Nome, Alaska:
- If a player hits a polar bear, he is penalized three strokes.
- If a player hits a polar bear and retrieves his ball, he is awarded five strokes.
Apparently those are local rules: In Extreme Golf, Duncan Lennard notes that officials of the World Ice Golf Championship actually wrote to the game’s governing body, the Royal and Ancient Golf Club of St Andrews, to ask what to do about polar bears, and received the ruling that “in the event of a polar bear wandering onto the ice golf course, the same safety procedure should be followed as for rattlesnakes and ants elsewhere in the world” — a free drop out of harm’s way.
“Juliet”
How did the party go in Portman Square?
I cannot tell you; Juliet was not there.
And how did Lady Gaster’s party go?
Juliet was next me and I do not know.
— Hilaire Belloc
Moving Day
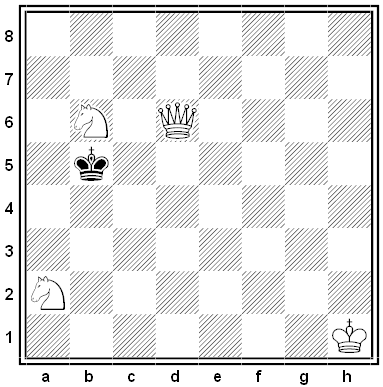
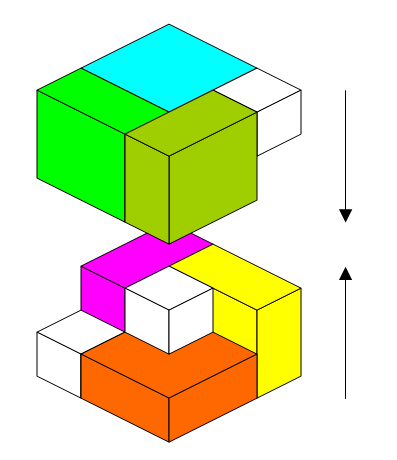
Is it possible to pack six 1 × 2 × 2 blocks and three 1 × 1 × 1 blocks into a 3 × 3 × 3 box?
Presto

Raymond Smullyan offered this proof at a conference on self-reference:
A: Santa Claus exists, if I am not mistaken.
B: Well, of course Santa Claus exists if you are not mistaken!
A: So I was right.
B: Yes.
A: So I was not mistaken.
B: Yes.
A: Hence, Santa Claus exists.
Character Study
Balzac’s 1829 treatise La physiologie du mariage contains a strange passage:

“Four editions of the book, three of them printed in Balzac’s lifetime, in fact contain four different versions,” notes F.L. Bauer in Decrypted Secrets. “The author must have been playing a practical joke on the reader. Nevertheless, [French military cryptanalyst Étienne] Bazeries investigated such a cryptogram in 1901 and found that it did not fit any known scheme; it was une facétie de l’auteur.”