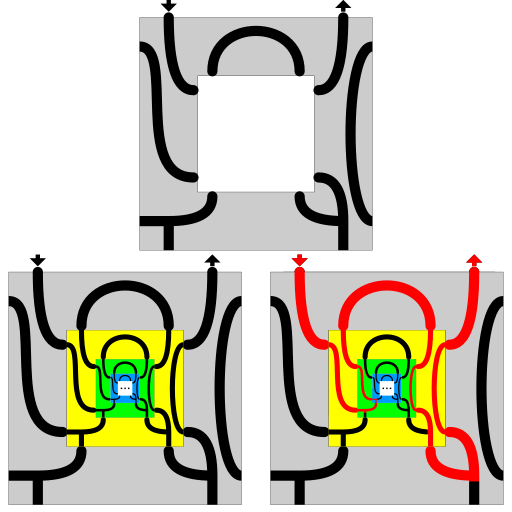
Above: A valid maze can be generated recursively by dividing an open chamber with walls and creating an opening at random within each wall, ensuring that a route can be found through the chamber. The secondary chambers themselves can then be divided with further walls, following the same principle, to any level of complexity.
Below: Valid mazes can even be generated fractally — here a solution becomes available in the third panel, but an unlucky solver might wander forever in the depths of self-similarity at the center of the image.