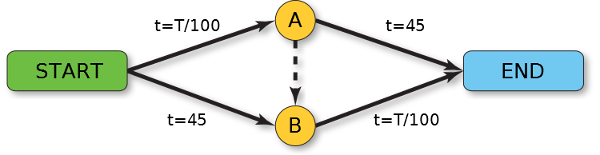
The diagram above represents a road network where T is the number of travelers. The leg from START to A takes T/100 = t minutes to traverse, as does the leg from B to END. The legs from START to B and from A to END each take a constant 45 minutes.
Now suppose that 4000 drivers want to travel from START to END. The northern and the southern routes are equally efficient, so the drivers will split into two groups, and each will arrive at END in 2000/100 + 45 = 65 minutes.
But now suppose that planners, hoping to improve matters, add a shortcut between A and B with a travel time of 0 minutes. Now all the drivers will take the route from START to A, since in the worst case it will take 4000/100 = 40 minutes, rather than the guaranteed 45 minutes taken by the leg from START to B. From A every driver will take the shortcut to B, for the same reason: Even in the worst case, the trip from B to END is 5 minutes faster than the trip from A to END.
As a result, every driver’s trip now takes 4000/100 + 4000/100 = 80 minutes, which is 15 minutes longer than in the original state of affairs. No individual driver has an incentive to change his behavior, since now the two original routes (northern and southern) each take 4000/100 + 45 = 85 minutes. If the 4000 drivers as a body could agree never to use the shortcut, they’d all be better off. But without a way to enforce this, all are stuck with longer commutes.
The principle was discovered by German mathematician Dietrich Braess in 1968. It’s known as Braess’ paradox.