
James Mason’s topiary park in downtown Columbus, Ohio, was inspired by Georges Seurat’s A Sunday Afternoon on the Island of La Grande Jatte, below.
So the image above is a photograph of a sculpture of a painting of a landscape.
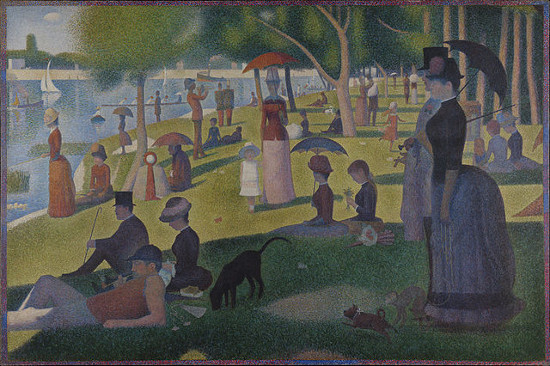

James Mason’s topiary park in downtown Columbus, Ohio, was inspired by Georges Seurat’s A Sunday Afternoon on the Island of La Grande Jatte, below.
So the image above is a photograph of a sculpture of a painting of a landscape.
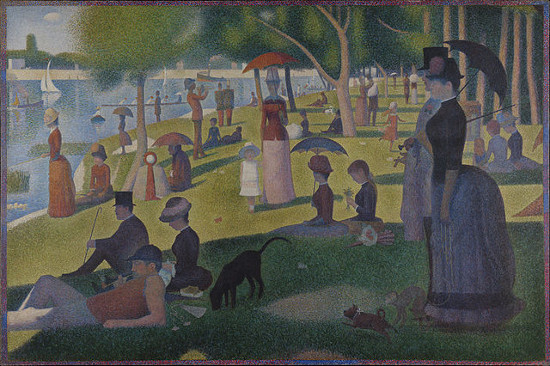
quisquilian
adj. worthless, trivial
noncurantist
adj. marked by indifference
diversivolent
adj. desiring strife
On April 18, 1930, in place of its 6:30 p.m. radio news bulletin, the BBC announced, “Good evening. Today is Good Friday. There is no news.” It filled the time with two minutes of piano music.
In 2010 computer programmer William Tunstall-Pedoe sifted 300 million facts about “people, places, business and events” and determined that April 11, 1954, was the single most boring day in the 20th century.
He told the Telegraph, “Nobody significant died that day, no major events apparently occurred and, although a typical day in the 20th century has many notable people being born, for some reason that day had only one who might make that claim — Abdullah Atalar, a Turkish academic.
“The irony is, though, that — having done the calculation — the day is interesting for being exceptionally boring. Unless, that is, you are Abdullah Atalar.”
(Thanks, Duncan.)

(Thanks, Brian and Breffni.)

A memorably phrased puzzle from The Graham Dial: “Consider a vertical girl whose waist is circular, not smooth, and temporarily at rest. Around the waist rotates a hula hoop of twice its diameter. Show that after one revolution of the hoop, the point originally in contact with the girl has traveled a distance equal to the perimeter of a square circumscribing the girl’s waist.”

Frightened villagers “killed” the first hydrogen balloon, launched in Paris by Jacques Charles and the Robert brothers Anne-Jean and Nicolas-Louis on Aug. 27, 1783. Allen Andrews, in Back to the Drawing Board: The Evolution of Flying Machines, quotes a contemporary account:
It is presumed that it was carried to a height of more than 20,000 feet, when it burst by the reaction of the Inflammable Gas upon the Atmospheric Air. It fell at three quarters past five near Gonesse, ten miles [actually, 15 miles] from the Field of Mars. The affrightened inhabitants ran together, appalled by the Hellish stench of sulphur, and two monks having assured them it was the skin of a Monstrous Animal, they attacked it with stones, pitchforks and flails. The Curate of the village was obliged to attend in order to sprinkle it with holy water and remove the fears of his astonished parishioners. At last they tied to the tail of a horse the first Instrument that was ever made for an Experiment in Natural Philosophy, and trained it across the field more than 6000 feet.
Perhaps forewarned, the first man to undertake a balloon flight in North America carried a pass from George Washington.

In 1943 three men came up with an ingenious plan to escape from the seemingly escape-proof Stalag Luft III prison camp in Germany. In this episode of the Futility Closet podcast we’ll learn about their clever deception, which made them briefly famous around the world.
We’ll also hear about the chaotic annual tradition of Moving Day in several North American cities and puzzle over how a severely injured hiker beats his wife back to their RV.
University of Strathclyde mathematician Adam McBride recalls that in his student days a particular teacher used to present a weekly puzzle. One of these baffled him:
Find positive integers a, b, and c, all different, such that a3 + b3 = c4.
“The previous puzzles had been relatively easy but this one had me stumped,” he wrote later. He created three columns headed a3, b3, and c4 and spent hours looking for a sum that would work. On the night before the deadline, he found one: 703 + 1053 = 354.
“This shows how sad a person I was! However, I then realised also how stupid I had been. I had totally missed the necessary insight.” What was it?

In 1948, as T.S. Eliot was departing for Stockholm to accept the Nobel Prize, a reporter asked which of his books had occasioned the honor.
Eliot said, “I believe it’s given for the entire corpus.”
The reporter said, “And when did you publish that?”
Eliot later said, “It really might make a good title for a mystery — The Entire Corpus.”
1. A puzzle from J.A.H. Hunter’s Fun With Figures, 1956:
Tom and Tim are brothers; their combined ages make up seventeen years. When Tom was as old as Tim was when Tim was twice as old as Tom was when Tom was fifteen years younger than Tim will be when Tim is twice his present age, Tom was two years younger than Tim was when Tim was three years older than Tom was when Tom was a third as old as Tim was when Tim was a year older than Tom was seven years ago. So how old is Tim?
2. Another, by Sam Loyd:
“How fast those children grow!” remarked Grandpa. “Tommy is now twice as old as Maggie was when Tommy was six years older than Maggie is now, and when Maggie is six years older than Tommy is now their combined ages will equal their mother’s age then, although she is now but forty-six.” How old is Maggie?
3. According to Wirt Howe’s New York at the Turn of the Century, 1899-1916, this question inspired an ongoing national debate when it appeared in the New York Press in 1903:
Brooklyn, October 12
Dear Tip:
Mary is 24 years old. She is twice as old as Anne was when she was as old as Anne is now. How old is Anne now? A says the answer is 16; B says 12. Which is correct?
John Mahon

Cornell mathematician Robert Connelly devised this intuition-defying card game. I shuffle a standard deck of 52 cards and deal them out in a row before you, one at a time. At some point before the last card is dealt, you must say the word “red.” If the next card I deal is red, you win $1; if it’s black you lose $1. If you play blind, your chance of winning is 1/2. Can you improve on this by devising a strategy that considers the dealt cards?
Surprisingly, the answer is no. Imagine a deck with two red cards and two black. Now there are six equally likely deals:
RRBB
RBBR
BBRR
RBRB
BRBR
BRRB
By counting, we can see that the chance of success remains 1/2 regardless of whether you call red before the first, second, third, or fourth card.
Trying to outsmart the cards doesn’t help. You might resolve to wait and see the first card: If it’s black you’ll call red immediately, and if it’s red you’ll wait until the fourth card. It’s true that this strategy gives you a 2/3 chance of winning if the first card is black — but if it’s red then it has a 2/3 chance of losing.
Similarly, it would seem that if the first two cards are black then you have a sure thing — the next card must be red. This is true, but it will happen only once in six deals; on the other five deals, calling red at the third card wins only 2/5 of the time — so this strategy has an overall success rate of (1/6 × 1) + (5/6 × 2/5) = 1/2, just like the others. The cards conspire to erase every seeming advantage.
The same principle holds for a 52-card deck, or indeed for any deck. In general, if a deck has r red cards and b black ones, then your chance of winning, by any strategy whatsoever, is r/(b + r). Seeing the cards that have already been dealt, surprisingly, is no advantage.
(Robert Connelly, “Say Red,” Pallbearers Review 9 [1974], 702.)