To pay for 1 frognab you’ll need at least four standard U.S. coins. To pay for 2, you’ll need at least six coins. But you can buy three with two coins. How much is 1 frognab?
Rolling Average

In a standard 10-frame game of bowling, the lowest possible score is 0 (all gutterballs) and the highest is 300 (all strikes). An average player falls somewhere between these extremes. In 1985, Central Missouri State University mathematicians Curtis Cooper and Robert Kennedy wondered what the game’s theoretical average score is — if you compiled the score sheets for every legally possible game of bowling, what would be the arithmetic mean of the scores?
It turns out it’s pretty low. There are (669)(241) possible games, which is about 5.7 × 1018. If we divide that into the total number of points scored in these games, we get
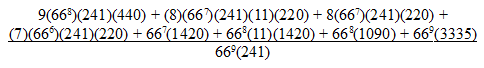
which is about 80 (79.7439 …).
This “might make you feel better about your average,” Cooper and Kennedy conclude. “The mean bowling score is indeed awful even if you are just an occasional bowler. Even though this information is interesting, there are more difficult questions about the game of bowling that could be asked. For example, you might wish to determine the standard deviation of the set of bowling scores and hence know more about the distribution of the set of all bowling scores. But the exact determination of the distibution of the set of scores is, in our opinion, a difficult problem. For example, given an integer k between 0 and 300, how many different bowling games have the score k? This, we leave as an open problem.”
(Curtis N. Cooper and Robert E. Kennedy, “Is the Mean Bowling Score Awful?”, Journal of Recreational Mathematics 18:3, 1985-86.)
Circle Ode
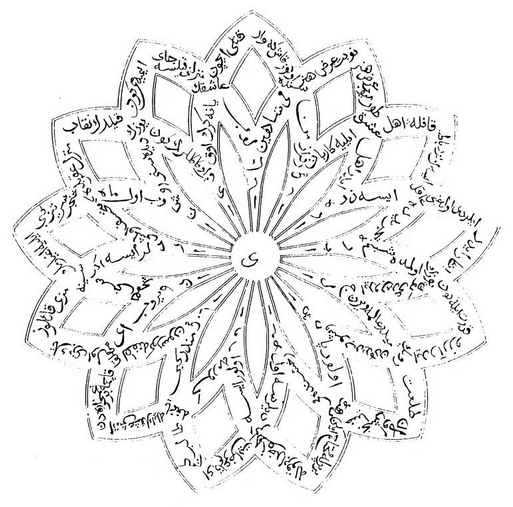
This love lyric was written by Shahin Ghiray (c. 1747-1787), the last sultan of the independent Crimea before its conquest by the Russians. It’s written in Turkish but in the Persian letter style of Arabic. The reader starts at the central letter and reads upward, which leads him into a series of arcs around the circle. Each arc forms a diptych that begins and ends with the central letter, and each line in the diptych intersects its neighbor so that they share a word.
Poet Dick Higgins writes, “When I asked a Persian student to read this for me, the sound, with its opening alliterations, was as much a tour de force as the visual aspect.” Unfortunately it’s hard to reflect all this in English; J.W. Redhouse attempted this translation in the Journal of the Royal Asiatic Society in 1861:
Let but my beloved come and take up her abode in the mansion of her lover, and shall not thy beautiful face cause his eyes to sparkle with delight!
Or, would she but attack my rival with her glances, sharp-pointed as daggers, and, piercing his breast, cause him to moan, as a flute is pierced ere it emit its sighing notes.
Turn not away, my beauty; nor flee from me, who am a prey to grief; deem it not fitting that I be consumed with the fire of my love for thee.
If the grace of God favour one of His servants, that man, from a state of utter destitution, may become the monarch of the world.
Tears flow from my eyes by reason of their desire to reach thee; for the sun of thy countenance, by an ordinance of the Almighty power, attracts to itself the moisture of the dew-drops.
If thou art wise, erect an inn on the road of self-negation; so that the pilgrims of holy love may make thereof their halting-place.
O proud and noble mistress of mine! with the eyebrows and glances that thou possessest, what need of bow or arrow wherewith to slay thy lover?
Is it that thou hast loosed thy tresses and veiled therewith the sun of thy countenance? Or is it that the moon has become eclipsed in the sign of Scorpio?
I am perfectly willing that my beloved should pierce my heart; only let that beauty deem me worthy of her favour.
Write, O pen! that I am a candidate for the flames, even as a salamander; declare it to be so, if that queen of beauty will it.
Is it the silvery lustre of the moon that has diffused brightness over the face of nature; or is it the sun of thy countenance that has illumined the world?
If any disputant should cavil, and deny the existence of thy beauty, would not thy adorer, hovering as a mote in its rays, suffice to convince the fool, if he had but common sense?
It is true that lovers do unremittingly dedicate their talents to the praise of their mistresses; but has thy turn yet come, Shahin-Ghiray, so to offer thy tribute of laudation?
Golomb Rulers
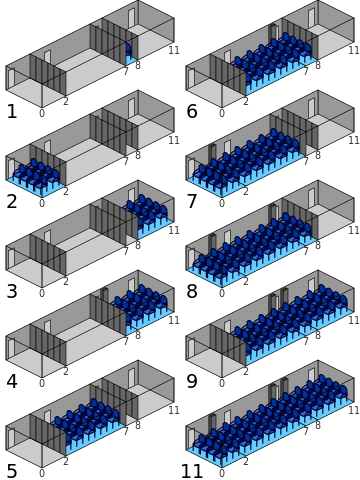
This conference room is 11 units long and has folding partitions at positions 2, 7, and 8. This gives it a curious property: For a meeting of any given size, the room can be configured in exactly one way. A meeting of size 6 must use partitions 2 and 8 — no other setup will work exactly.
This is an example of a Golomb ruler, named for USC mathematician Solomon Golomb. It’s called a ruler because the simplest example is a measuring stick: If we’re given a 6-centimeter ruler, we find that we can add 4 marks (at integer positions) so that no two of them are the same distance apart: 0 1 4 6. No shorter ruler can accommodate 4 marks without duplication, so the 0-1-4-6 ruler is said to be “optimal.” It’s also “perfect” because it can measure any distance from 1 to 6.
The conference room is optimal because no shorter room can accommodate 5 walls without equal-sized partitions becoming available, but it’s not perfect, because it can’t accommodate an assembly of size 10. (It turns out that no perfect ruler with five marks is possible.)
Finding optimal Golomb rulers is hard — simply extending an existing ruler tends to produce a new ruler that’s either not Golomb or not optimal. The only way forward, it seems, is to compare every possible ruler with n marks and note the shortest one, an immensely laborious process. Distributed computing projects have found the longest optimal rulers to date — the most recent, with 27 marks, was found in February, five years after the previous record.
First Impressions

Shortly before its orchestral premiere in 1885, Johannes Brahms performed his fourth symphony for a small private audience in an arrangement for two pianos, played by himself and Ignaz Brüll.
After the first movement Brahms paused to assess its effect, and critic Eduard Hanslick, who was turning the pages, said, “For the whole movement I had the feeling that I was being given a beating by two incredibly intelligent people.”
Far From Home

This is a detail from the allegorical painting Taste, Hearing and Touch, completed in 1620 by the Flemish artist Jan Brueghel the Elder. If the bird on the right looks out of place, that’s because it’s a sulphur-crested cockatoo, which is native to Australia. The same bird appears in Hearing, painted three years earlier by Brueghel and Peter Paul Rubens.
How did an Australian bird find its way into a Flemish painting in 1617? Apparently it was captured during one of the first Dutch visits to pre-European Australia, perhaps by Willem Janszoon in 1606, who would have carried it to the Dutch East Indies (Indonesia) and then to Holland in 1611. That’s significant — previously it had been thought that the first European images of Australian fauna had been made during the voyages of William Dampier and William de Vlamingh, which occurred decades after Brueghel’s death in 1625.
Warwick Hirst, a former manuscript curator at the State Library of New South Wales, writes, “While we don’t know exactly how Brueghel’s cockatoo arrived in the Netherlands, it appears that Taste, Hearing and Touch, and its precursor Hearing, may well contain the earliest existing European images of a bird or animal native to Australia, predating the images from Dampier’s and de Vlamingh’s voyages by some 80 years.”
(Warwick Hirst, “Brueghel’s Cockatoo,” SL Magazine, Summer 2013.) (Thanks, Ross.)
Podcast Episode 33: Death and Robert Todd Lincoln

Abraham Lincoln’s eldest son, Robert, is the subject of a grim coincidence in American history: He’s the only person known to have been present or nearby at the assassinations of three American presidents. In the latest Futility Closet podcast we describe the circumstances of each misfortune and explore some further coincidences regarding Robert’s brushes with fatality.
We also consider whether a chimpanzee deserves a day in court and puzzle over why Australia would demolish a perfectly good building.
Warnsdorff’s Rule
The knight’s tour is a familiar task in chess: On a bare board, find a path by which a knight visits each of the 64 squares exactly once. There are many solutions, but finding them by hand can be tricky — the knight tends to get stuck in a backwater, surrounding by squares that it’s already visited. In 1823 H.C. von Warnsdorff suggested a simple rule: Always move the knight to a square from which it will have the fewest available subsequent moves.
This turns out to be remarkably effective: It produces a successful tour more than 85% of the time on boards smaller than 50×50, and more than 50% of the time on boards smaller than 100×100. (Strangely, on a 7×7 board its success rate drops to 75%; see this paper.) The video above shows a successful tour on a standard chessboard; here’s another on a 14×14 board:
While we’re at it: British puzzle expert Henry Dudeney once set himself the task of devising a complete knight’s tour of a cube each of whose sides is a chessboard. He came up with this:
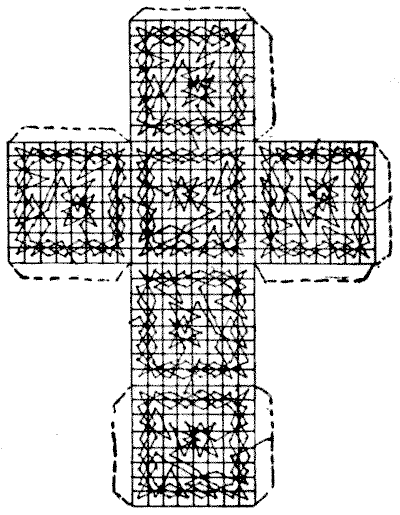
If you cut out the figure, fold it into a cube and fasten it using the tabs provided, you’ll have a map of the knight’s path. It can start anywhere and make its way around the whole cube, visiting each of the 364 squares once and returning to its starting point.
Dudeney also came up with this puzzle. The square below contains 36 letters. Exchange each letter once with a letter that’s connected with it by a knight’s move so that you produce a word square — a square whose first row and first column comprise the same six-letter word, as do the second row and second column, and so on.
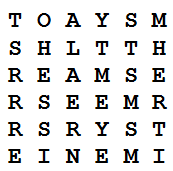
So, for example, starting with the top row you might exchange T with E, O with R, A with M, and so on. “A little thought will greatly simplify the task,” Dudeney writes. “Thus, as there is only one O, one L, and one N, these must clearly be transferred to the diagonal from the top left-hand corner to the bottom right-hand corner. Then, as the letters in the first row must be the same as in the first file, in the second row as in the second file, and so on, you are generally limited in your choice of making a pair. The puzzle can therefore be solved in a very few minutes.”
In a Word
ingram
n. one who is ignorant
stupex
n. a stupid person
ignotism
n. a mistake due to ignorance
incogitant
adj. that does not think
insulse
adj. lacking wit or sense
crassitude
n. gross ignorance or stupidity
parviscient
adj. knowing little; ignorant
antisocordist
n. an opponent of sloth or stupidity
Different Strokes

G.H. Hardy had a famous distaste for applied mathematics, but he made an exception in 1945 with an observation about golf. Conventional wisdom holds that consistency produces better results in stroke play (where strokes are counted for a full round of 18 holes) than in match play (where each hole is a separate contest). So if two players complete a full round with the same total number of strokes, then the more erratic player should do better if they compete hole by hole.
Hardy argues that the opposite is true. Imagine a course on which every hole is par 4. Player A is so deadly reliable that he shoots par on every hole. Player B has some chance x of hitting a “supershot,” which saves a stroke, and the same chance of hitting a “subshot,” losing a stroke. Otherwise he shoots par. Both players will average par and will be equal over a series of full rounds of golf, but the conventional wisdom says that B’s erratic play should give him an advantage if they play each hole as a separate contest.
Hardy’s insight is that the presence of the hole limits a run of good luck, while there’s no such limit on a run of bad luck. “To do a three, B must produce a supershot at one of his first three strokes, while he will take a five if he makes a subshot at one of his first four. He will thus have a net expectation 4x – 3x of loss on the hole, and should lose the match, contrary to common expectation.”
In general he finds that B’s chance of winning a hole is 3x – 9x2 + 10x3, and his chance of losing is 4x – 18x2 + 40x3 – 35x4, so that there’s a balance f(x) = x – 9x2 + 30x3 – 35x4 against him. If x < 0.37 -- that is, in all realistic cases -- the erratic player should lose. "If experience points the other way -- and I cannot deny it, since I am no golfer -- what is the explanation? I asked Mr. Bernard Darwin, who should be as good a judge as one could find, and he put his finger at once on a likely flaw in the model. To play a 'subshot' is to give yourself an opportunity of a 'supershot' which a more mechanical player would miss: if you get into a bunker you have an opportunity of recovering without loss, and one which you are naturally keyed up to take. Thus the less mechanical player's chance of a supershot is to some extent automatically increased. How far this may resolve the paradox, if it is one, I cannot say, and changes in the model make it unpleasantly complex." (G.H. Hardy, "A Mathematical Theorem About Golf," Mathematical Gazette, December 1945.)

