macrotous
adj. having large ears
capitose
adj. large-headed
dolichoderous
adj. long-necked
ventripotent
adj. having a large belly
dolichopodous
adj. having long feet
sciapodous
adj. “That resembles the Sciapodes; having very large feet.”

macrotous
adj. having large ears
capitose
adj. large-headed
dolichoderous
adj. long-necked
ventripotent
adj. having a large belly
dolichopodous
adj. having long feet
sciapodous
adj. “That resembles the Sciapodes; having very large feet.”
We’ve mentioned before that you can estimate π by dropping needles on the floor. (Reader Steven Karp also directed me to this remarkable solution, from Daniel A. Klain and Gian-Carlo Rota’s Introduction to Geometric Probability [1997].)
Here’s a related curiosity. If a circle of diameter L is placed at random on a pattern of circles of unit diameter, which are arranged hexagonally with centers C apart, then the probability that the placed circle will fall entirely inside one of the fixed circles is
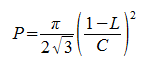
If we put k = C/(1 – L), we get
![]()
And a frequency estimate of P will give us an estimate of π.
Remarkably, in 1933 A.L. Clarke actually tried this. In Scripta Mathematica, N.T. Gridgeman writes:
His circle was a ball-bearing, and his scissel a steel plate. Contacts between the falling ball and the plate were electrically transformed into earphone clicks, which virtually eliminated doubtful hits. With student help, a thousand man-hours went into the accumulation of N = 250,000. The k was about 8/5, and the final ‘estimate’ of π was 3.143, to which was appended a physical error of ±0.005.
“This is more or less the zenith of accuracy and precision,” Gridgeman writes. “It could not be bettered by any reasonable increase in N — even if the physical error could be reduced, hundreds of millions of falls would be needed to establish a third decimal place with confidence.”
(N.T. Gridgeman, “Geometric Probability and the Number π,” Scripta Mathematica 25:3 [November 1960], 183-195.)

When my brother and I built and flew the first man-carrying flying machine, we thought that we were introducing into the world an invention which would make further wars practically impossible. That we were not alone in this thought is evidenced by the fact that the French Peace Society presented us with medals on account of our invention. We thought governments would realize the impossibility of winning by surprise attacks, and that no country would enter into war with another of equal size when it knew that it would have to win by simply wearing out its enemy.
— Orville Wright to C.M. Hitchcock, June 21, 1917

In 1855 Pedro Carolino decided to write a Portuguese-English phrasebook despite the fact that he didn’t actually speak English. The result is one of the all-time masterpieces of unintentional comedy, a language guide full of phrases like “The ears are too length” and “He has spit in my coat.” In this episode of the Futility Closet podcast we’ll sample Carolino’s phrasebook, which Mark Twain called “supreme and unapproachable.”
We’ll also hear Hamlet’s “to be or not to be” rendered in jargon and puzzle over why a man places an ad before robbing a bank.
A puzzle from J.A.H. Hunter’s Fun With Figures (1956):
A man paddling a canoe upstream sees a glove in the water as he passes under a bridge. Fifteen minutes later, he turns around and paddles downstream. He passes under the bridge and travels another mile before reaching the rock from which he started, which the glove is just passing. If he paddled at the same speed the whole time and lost no time in turning around, what is the speed of the current?

In 1940, just before the release of her film They Knew What They Wanted, Carole Lombard’s press agent, Russell Birdwell, approached the filmmakers with a novel publicity scheme. Lombard would be scheduled to fly to New York for the opening, but they would arrange for the plane to “go down” en route and remain missing for 12 hours.
“And in those twelve hours, fellas, we’re going to be on every goddam front page in the United States of America,” Birdwell said. “Not only Carole Lombard’s name, but the name of the picture and the name of the theatre it’s going to open at and how would you like to foot the bill for that kind of advertising?” He planned that eventually Lombard and the pilot could wander out of the woods saying that the plane’s engines and radio had died.
In his 1967 memoir Hollywood, director Garson Kanin remembers that in the meeting Lombard began to slap her thigh, yelling, “I’ll die! I’ll die! Isn’t that something? I’ll die!”
Birdwell’s plan was considered seriously but finally canceled due to the cost. Two years later, Lombard died in a plane crash in Nevada. “I could hear Carole’s voice and the sound of her hand slapping her thigh, her voice yelling delightedly, ‘I’ll die! I’ll die!'” Kanin wrote. “I remembered Russell Birdwell’s notion of the fake crash for publicity. I stood there hoping against hope that perhaps this was a postponed version of his scheme. … Carole Lombard … could not be dead at thirty-five. But she was.”
(Thanks, Ted.)
In his 1607 Rich Storehouse, or Treasurie for the Diseased, Matthew Blower offers “a present medicine for the hickop”:
Take thy finger ends, and stop both thine ears very hard, and the hickop will surcease immediately.
I found this in Julian Walker’s How to Cure the Plague and Other Curious Remedies (2013), a collection of historical cures for various maladies. He says, “I tried it, and it worked.”
One of democracy’s ideals is egalitarianism: Each person gets one vote, and all votes are equally consequential, so that all people have equal power over the world. For that reason we consider it improper for one person to vote twice in the same election. But then shouldn’t we also consider it improper for dual citizens to cast votes in two different places?
It’s true that dual citizens vote in different elections, but they’re still exercising twice as much power over the world as other voters. And it’s true that power is already unequally distributed among the world’s voters, but this is no reason to shrink from the ideal.
The fact that a dual citizen has the legal right to cast two ballots doesn’t mean that this accords with democratic principles. Suppose that Texas passed a law saying that any native-born Texan can vote in Texas, regardless of where he currently lives. Then a Texan living in Pennsylvania could cast ballots in both states, whereas a native Pennsylvanian could vote only once. This might be legal, but we would object morally to the unfairness of such a law.
Given the unequal influence of the world’s nations, one idealistic way to equalize power among all voters would be to give everyone a right to vote in every election, everywhere. This would give each of us an equal amount of power over the world. “That vision remains pretty visionary, we concede,” write Robert E. Goodin and Ana Tanasoca. “Still, visions matter.”
(Robert E. Goodin and Ana Tanasoca, “Double Voting,” Australasian Journal of Philosophy, vol. 92, no. 4, 743-758.)
Eleven fenmen from the Isle of Ely, being employed by Sir John Griffin, in training a part of his park at Audley End, went one evening to the Inn called The Hoops, to drink. After getting a little spirited, they told the maid, they would give sixpence each to fetch them as much beer they could drink, in half-pints out of the cellar; if they tired her, she was to pay for the liquor; if she tired them, they were to pay for the whole. The girl accepted the bet, although she had been washing all the day, and drew them 517 single half-pints, before they gave out, which were all drank by the said men. The distance from the room where they sat, to the tap, was measured, from which it appears she walked near 12 miles in fetching it; and the quantity of liquor drank by each man was about three gallons in three hours. The above is the real fact.
— Police Gazette, Feb. 17, 1775
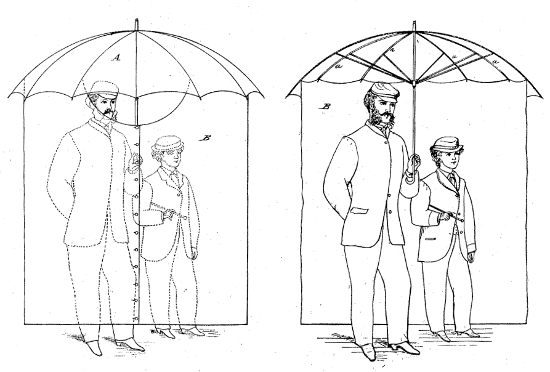
An ordinary umbrella wasn’t enough for Elizur E. Clarke — in 1864 he suggested adding a skirt, to render it “a more perfect protector from storms.”
The man gets a little loophole to look out of. His companion will just have to trust him.