In a Word

bunnikin
n. an early flower
Already now the Snowdrop dares appear,
The first pale blossom of the unripened year:
As Flora’s breath, by some transforming power,
Had changed an icicle into a flower:
Its name and hue the scentless plant retains
And Winter lingers in its icy veins.
— Anna Laetitia Barbauld (1743-1825)
Asked and Answered
Novelist Simon Raven was known as a bit of a bounder.
When his wife wired him WIFE AND BABY STARVING SEND MONEY SOONEST, he cabled back SORRY NO MONEY SUGGEST EAT BABY.
The Ulysses Contract

In 1982, 24-year-old schizophrenic patient J.S. faced a difficult decision: The neuroleptic drug Prolixin relieved his psychotic symptoms, but it produced tardive dyskinesia, a progressive disorder that caused uncontrollable movements of his legs, arms, and tongue.
His therapist learned of an experimental program that might reduce this side effect, and J.S. signed consent forms to enter treatment. But the first step was to stop all medications, and without the Prolixin he descended again into psychosis and refused the experimental medication.
This produces an impossible dilemma: Does J.S.’ “sane” self have the right to overrule his “insane” self, if the two disagree? Can Dr. Jekyll bind Mr. Hyde? Such a directive is sometimes called a Ulysses contract, after the Greek hero who ordered his men to disregard his commands as they sailed past the sirens. If a patient directs his caregivers to ignore his own future requests, can the caregivers follow these orders?
In J.S.’ case, the answer was no. The research unit’s legal counsel decided that his earlier consent did not override his later refusal, and he was withdrawn from the program. When he resumed his antipsychotic medication and learned what had happened, he begged for another chance to try the experimental medication. Had they been wrong to refuse him?
(Morton E. Winston, Sally M. Winston, Paul S. Appelbaum, and Nancy K. Rhoden, “Can a Subject Consent to a ‘Ulysses Contract’?”, The Hastings Center Report 12:4 [August 1982], 26-28.)
“At Eventide”
Goo-goo goo-goo goo-goo goo
Goo-goo goo-goo goo-goo
Googly, googly, googly goo:
That’s how we fill a column.
— G.K. Chesterton
Shock Tactics
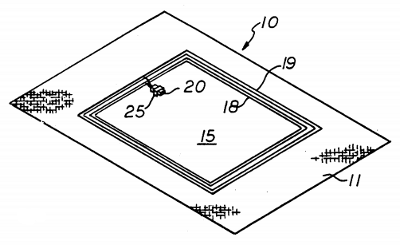
Here’s one way to prevent ants from ruining your picnic — surround the tablecloth with parallel strips of electrically conductive material and attach them to a DC battery. Now any bug that crosses the border will close the circuit and get “a sensation which will discourage further travel across the edge of the cloth.” (Humans will feel only “a slight tingling sensation.”)
This idea, patented by Richard Mahan in 1992, has a proud history — Thomas Edison tried essentially the same thing as a young man.
The Rolling Die

Imagine a die that exactly covers one square of a checkerboard. Place the die in the top left corner with the 6 uppermost. Now, by tipping the die over successively onto each new square, can you roll it through each of the board’s 64 squares once and arrive in the upper right, so that the 6 is exposed at the beginning and end but never elsewhere?
Appearances

Costa Rica’s alligator bug, Fulgora laternaria, bears a protuberance that looks remarkably like a caiman’s head — a feature that may make a hungry bird think twice.
The leaf insects of Southeast Asia, below, so convincingly mimic living leaves that they even bear “bite marks.” This fooled Magellan’s companion Antonio Pigafetta, who encountered them in the Philippines in 1521:
In this island are also found certain trees, the leaves of which, when they fall, are animated, and walk. They are like the leaves of the mulberry tree, but not so long; they have the leaf stalk short and pointed, and near the leaf stalk they have on each side two feet. If they are touched they escape, but if crushed they do not give out blood. I kept one for nine days in a box. When I opened it the leaf went round the box. I believe they live upon air.

Perspective

In a photograph, is there a way to distinguish between a landscape and its reflection?
The Ship of Theseus

Suppose we have a complete wooden ship, and one day we replace one of its wooden planks with an aluminum one. Most people would agree that the ship survives this operation; that is to say, its identity remains unchanged. But suppose that we then replace a second plank, and then a third, until our wooden ship is made entirely of aluminum. Is this the same ship that we started with? If not, when did it change?
Thomas Hobbes adds a wrinkle: Suppose that, as we did all this refurbishing, someone had gathered up all the discarded wooden planks and used them to assemble a second ship. What are we to make of this? “This, without doubt, had also been the same numerical ship with that which was at the beginning; and so there would have been two ships numerically the same, which is absurd.”
And philosopher Roderick Chisholm adds another: “Let us suppose that the captain of the original ship had solemnly taken the vow that, if his ship were ever to go down, he would go down with it. What, now, if the two ships collide at sea and he sees them start to sink together? Where does his duty lie — with the aluminum ship or with the reassembled wooden ship?”
See Jeannot’s Knife.