David B. Lewis’ 1983 book Eureka!: Math Fun From Many Angles begins with this notice:
Errata
1. There are no mistakes in this book. The above should read ‘Erratum.’
Is the correction a mistake or not?
David B. Lewis’ 1983 book Eureka!: Math Fun From Many Angles begins with this notice:
Errata
1. There are no mistakes in this book. The above should read ‘Erratum.’
Is the correction a mistake or not?
In 1819, as the Bank of England struggled against counterfeiters, T.C. Hansard proposed a note that combined such a variety of typefaces that a lone forger couldn’t hope to duplicate it — the faces descended all the way to Diamond, the smallest available, and the bottom of each note would be filled with 140 lines of fine print containing hidden “private marks,” such as individual letters printed in italic or small capitals.
To create even the authentic version would have required a team of 20 people, from punchcutters to engine makers, to fulfill the typographical and other design flourishes. Hansard estimated that producing the first note would have cost as much as £2,000 and taken up to a year, “but after that the production will be so rapid, that with the labour of four Men only, without the assistance of any Steam Machinery, 40,000 Notes may be produced in a Day of the finest Workmanship, at the Expense, including Paper, of Half a Farthing each Note.”
In the end the proposal wasn’t adopted — small notes were withdrawn from circulation in 1821, and the search was dropped.
(Virginia Hewitt, “Beware of Imitations: The Campaign for a New Bank of England Note, 1797-1821,” Numismatic Chronicle 158 [1998], 197-222.)

During the middle ages there existed a monastery, in which lived twenty-four monks, presided over by a blind abbot. The cells of the monastery were planned as shown in the accompanying figure, passages being arranged along two sides of each of the outer cells and all round the inner cell, in which the abbot took up his quarters. Three monks were allotted to each cell, making, of course, nine monks in each row of cells. The abbot, being lazy as well as blind, was very remiss in making his rounds, but provided he could count nine heads on each side of the monastery he retired into his own cloister, contented and satisfied that the monks were all within the building, and that no outsiders were keeping them company. The monks, however, taking advantage of their abbot’s blindness and remissness, conspired to deceive him, a portion of their number sometimes going out and at other times receiving friends in their cells. They accomplished their deception, and it never happened that strangers were admitted when monks were out, yet there never were more nor less than nine persons upon each side of the building. Their first deception consisted in four of their number going out, upon which four monks took possession of each of the cells numbered 1, 3, 6, and 8, one monk only being left in each of the other cells; nine monks being thus on each side of the building. Upon returning, the four monks brought in four friends, when it was necessary to arrange the twenty-eight persons, two in each of the cells 1, 3, 6, and 8, and five in each of the others; still nine heads only were to be counted in either row. Emboldened by success, eight outsiders were introduced, and the thirty-two persons now were arranged, one only in each of the cells 1, 3, 6, and 8, but seven in each of the other cells; again, according to the abbot’s system of counting, all was well. In the next endeavour, the strangers all went away and took six monks with them, leaving but eighteen at home to represent twenty-four; these eighteen placed themselves five in each of the cells 1 and 8 and four in each of the cells 3 and 6; the remaining cells were empty, but the cells on each side of the building still contained nine monks. On returning, the six truants each brought two friends to pass the night, and the thirty-six retired to rest, nine in each of the cells 2, 4, 5, and 7; the remainder were empty, and the abbot was quite satisfied that the monks were alone in the monastery.
— Cassell’s Book of In-Door Amusements, Card Games and Fireside Fun, 1882
I loved thee, beautiful and kind,
And plighted an eternal vow;
So alter’d are thy face and mind,
‘Twere perjury to love thee now.
— Robert, Earl Nugent (1709-1788)
Has it ever occurred to you that novelists are using up experience at a dangerous rate? No, I see it hasn’t. Well, then, consider that before the novel emerged as the dominant literary form, narrative literature dealt only with the extraordinary or the allegorical — with kings and queens, giants and dragons, sublime virtue and diabolic evil. There was no risk of confusing that sort of thing with life, of course. But as soon as the novel got going, you might pick up a book at any time and read about an ordinary chap called Joe Smith doing just the sort of things you did yourself. Now, I know what you’re going to say — you’re going to say that the novelist still has to invent a lot. But that’s just the point: there’ve been such a fantastic number of novels written in the past couple of centuries that they’ve just about exhausted the possibilities of life. So all of us, you see, are really enacting events that have already been written about in some novel or other.
— David Lodge, The British Museum Is Falling Down, 1965

In the 1980s, when Nicolae Ceauşescu set about razing central Bucharest, engineer Eugeniu Iordăchescu was despairing the threat to the area’s iconic churches when he saw a waiter carrying a tray of drinks. “I saw that the secret of the glasses not falling was the tray,” he said, “so I started trying to work out how to apply a tray to the building.”
He hit on a method of digging beneath the buildings to insert reinforced concrete supports, then rolling them to new locations using hydraulic levers and mechanical pulleys. Over a period of six years, his team saved more than a dozen churches and other buildings that the Communists had planned to destroy; the 800-ton Schitul Maicilor, above, was moved almost 270 yards from its 18th-century foundations.
The technique Iordăchescu pioneered is still in use today. “He was very proud of his achievements, and even in retirement he spent a lot of time improving and helping others to push the method further on,” his son Nicholas told the New York Times. “He will be remembered for a one-of-a-kind contribution to developing this technology.”
(Thanks, Jason.)

The Feuer Buech, a 1584 treatise on munitions by Franz Helm, contains a startling illustration: a cat and a bird approaching a town, each bearing a lighted explosive.
The image accompanies a section titled “To set fire to a castle or city which you can’t get at otherwise”; Penn curator Mitch Fraas translates the relevant section:
Create a small sack like a fire-arrow … if you would like to get at a town or castle, seek to obtain a cat from that place. And bind the sack to the back of the cat, ignite it, let it glow well and thereafter let the cat go, so it runs to the nearest castle or town, and out of fear it thinks to hide itself where it ends up in barn hay or straw it will be ignited.
Fortunately it appears this was never carried into practice … though possibly birds have been used for this purpose in Russia.
rarachose
adj. rare, unusual
selcouth
adj. extraordinary in appearance
cordate
adj. heart-shaped
trothplight
n. engagement to be married
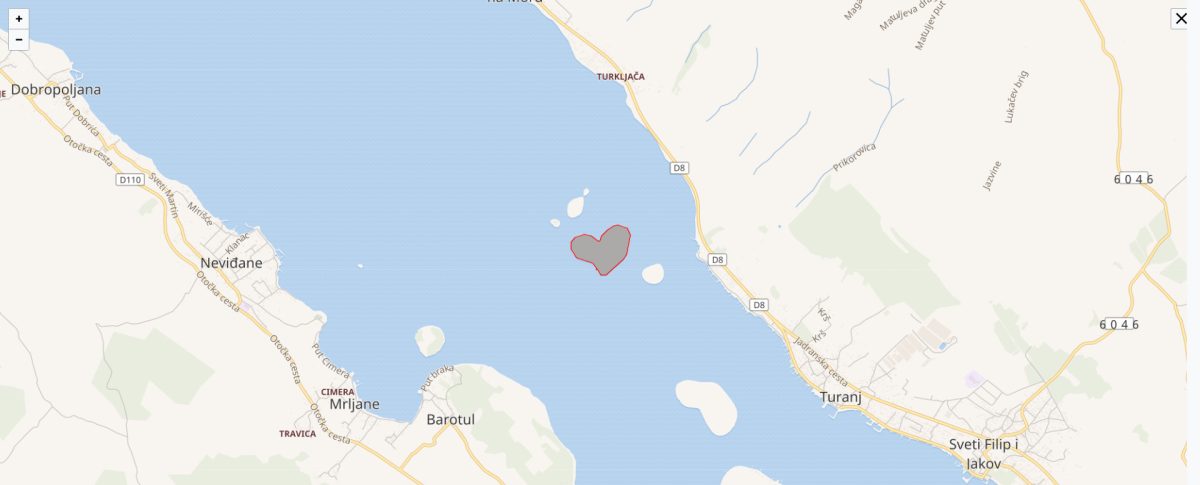
The Croatian islet Galešnjak, in the Pašman Canal of the Adriatic Sea, is one of the few naturally occurring heart-shaped objects in the world.
It’s uninhabited, but the family that owns it provides facilities for engagements and weddings.

An arrow has a 1/4 chance of hitting its target. If four arrows are shot at one target, what’s the chance that the target will be hit?

Here’s a checkerboard. Suppose we put a checker on each of the nine squares in the lower left corner. And suppose that any checker can move in any direction by jumping over an adjacent checker, provided that the square beyond it is vacant. Is there some combination of moves by which we can transfer the nine checkers to the nine squares in the upper left corner of the board?