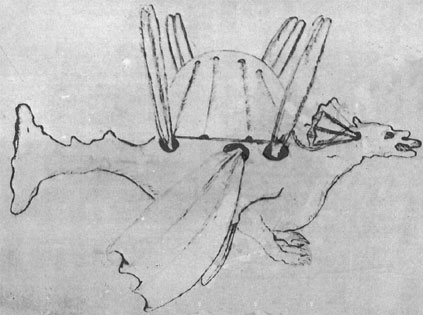
In 1647, Venetian inventor Tito Livio Burattini built a flying machine that could carry a cat. Reportedly the vessel had four pairs of wings and was driven by cords pulled by hand; it “remained airborne as long as a man kept the feathers and wheels in motion by the way of a string.” One observer wrote, “if the cat had the understanding to do that — its strength would be sufficient for this — it would keep itself in the air.”
This 4-foot “Dragon Volant” was only a prototype; Burattini hoped to produce a finished version that could carry a man. By May 1648 he’d brought out an improved model, and German polymath Johann Joachim Becher even mentions a report that the aircraft eventually rose into the air with three people aboard, including the inventor, who “wanted to fly from Warsaw to Constantinople inside 12 hours.” But “as there were always some shortcomings, perfection was never achieved,” and it appears the project ended there.
(Jerzy B. Cynk, Polish Aircraft, 1893-1939, 1971.)