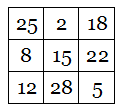
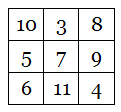
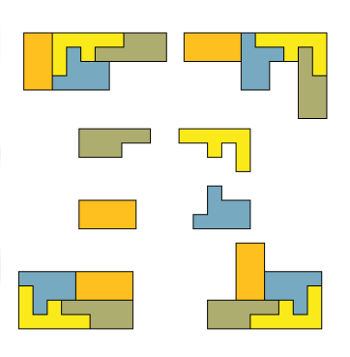
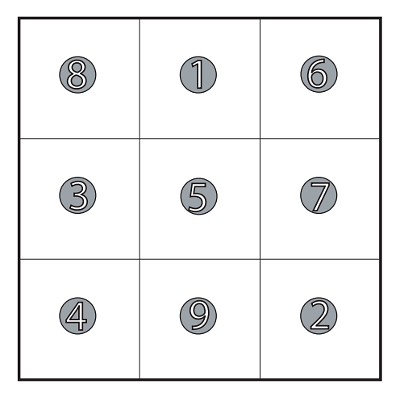
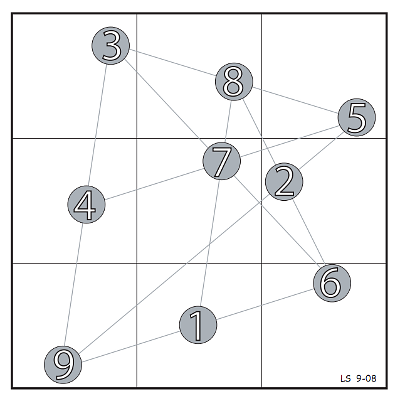
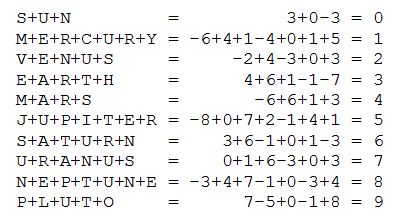Only the brilliantly inventive Lee Sallows would think of this. The figure above combines Penrose triangles with Borromean rings: Each of the triangles is an impossible object, and they’re united in a perplexing way — although the three are linked together, no two are linked.
(Thanks, Lee.)