
George Burns made no movies between Honolulu in 1939 and The Sunshine Boys in 1975.
When Esquire asked why, he said, “My agent was afraid of overexposure.”

George Burns made no movies between Honolulu in 1939 and The Sunshine Boys in 1975.
When Esquire asked why, he said, “My agent was afraid of overexposure.”
This is a story of four brothers. Billy owed a dollar to Jerry. Jerry owed a dollar to Tommy, and Tommy owed a dollar to Billy. The three of them met one day at a family picnic. Being brothers and good friends, none wished to hound the other about his debt. Vincent, the fourth brother, arrived at the picnic with some beer. While he was busily unloading the truck, Billy walked over, unnoticed, and quietly asked Vincent for a loan of a dollar, which Vincent gladly gave to him. Billy then ambled over to Jerry and paid him the dollar he owed him; then Jerry paid Tommy the dollar he owed to him; Tommy then went over to Billy and paid him the dollar he owed him. Billy then walked back to Vincent and paid him back his dollar. All old debts were paid. Simple, isn’t it?
— Raymond F. Lausmann, Fun With Figures, 1965
The one-L lama,
He’s a priest.
The two-L llama,
He’s a beast.
And I would bet
A silk pajama
There isn’t any
Three-L lllama.
When Ogden Nash published this poem, a reader pointed out that a large fire in Boston is a three-alarmer.
Nash responded, “Pooh.”

Prince Charming tells Sleeping Beauty, “I’m going to put you to sleep with this potion, and then I’ll flip a coin. Today is Sunday. If the coin lands heads, I’ll wake you again on Monday. If it lands tails, then I’ll wake you on Monday, put you to sleep again, and wake you on Tuesday. The potion induces a mild amnesia, so you won’t remember the intermediate awakening if it happens, but otherwise it won’t hurt you.”
When Sleeping Beauty awakes, what probability should she assign that the coin landed heads?
There seem to be two contradictory answers to this. From one perspective, the coin was fair, so it would seem the chance is 1/2. But from another, Beauty finds herself in one of three equally likely situations (heads/Monday, tails/Monday, and tails/Tuesday), so the chance of heads appears to be 1/3. Which is correct?

“My books are water; those of the great geniuses are wine. Everybody drinks water.” — Mark Twain
Jim finds himself in the central square of a small South American town. Tied up against the wall are a row of twenty Indians, most terrified, a few defiant, in front of them several armed men in uniform. A heavy man in a sweat-stained khaki shirt turns out to be the captain in charge and, after a good deal of questioning of Jim which establishes that he got there by accident while on a botanical expedition, explains that the Indians are a random group of inhabitants who, after recent acts of protest against the government, are just about to be killed to remind other possible protestors of the advantages of not protesting. However, since Jim in an honoured visitor from another land, the captain is happy to offer him a guest’s privilege of killing one of the Indians himself. If Jim accepts, then as a special mark of the occasion, the other Indians will be let off. Of course, if Jim refuses, then there is no special occasion, and Pedro here will do what he was about to do when Jim arrived, and kill them all. Jim, with some desperate recollection of schoolboy fiction, wonders whether if he got hold of a gun, he could hold the captain, Pedro and the rest of the soldiers to threat, but it is quite clear from the set-up that nothing of that kind is going to work: any attempt at that sort of thing will mean that all the Indians will be killed, and himself. The men against the wall, and the other villagers, understand the situation, and are obviously begging him to accept. What should he do?
— Bernard Williams, “A Critique of Utilitarianism,” from Utilitarianism: For and Against, 1973
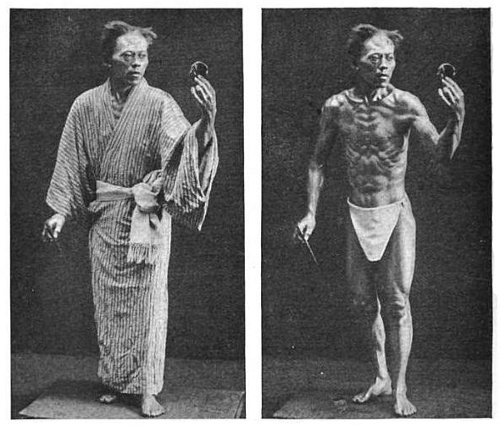
Which of these is Japanese sculptor Hananuma Masakichi, and which is the life-size wooden statue he completed in 1885? Amazingly, the statue’s on the right. Masakichi spent three years posing between two adjustable mirrors to capture every skin blemish, blue vein, and discoloration on his body, even inserting his own body hairs into hand-drilled holes at precise locations. He added glass eyes and eyelashes that were exact facsimiles of his own and applied a coat of lacquer to give the finished statue the appearance of flesh and blood. The finished product is so convincing that crowds reportedly had difficulty distinguishing the artist from his work when he posed next to it at exhibition. “The figure stands with a little mask in one hand and an instrument for carving in the other,” reported the Oriental Review. “The lifelike eyes are apparently gazing at the mask, and the face wears a look of intense absorption.”
A man hired by John Smith and Co.
Loudly declared that he’d tho.
Men that he saw
Dumping dirt near his store;
The drivers, therefore, didn’t do.
There is an old cook in N.Y.
Who insists you should always st.p.
Full vainly he’s tried
To eat some that was fried,
But he says he would rather ch.c.
The sermon our pastor Rt. Rev.
Began may have had a rt. clev.,
But his talk, though consistent,
Kept the end so far distant
That we left, since we felt he mt. nev.
— Anonymous
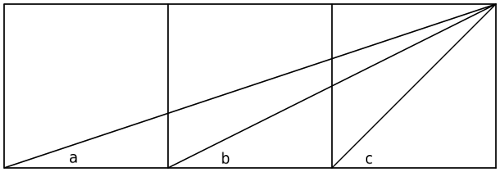
Given three adjacent squares,
a + b = c.
“Beauty is the first test,” wrote G.H. Hardy. “There is no permanent place in the world for ugly mathematics.”
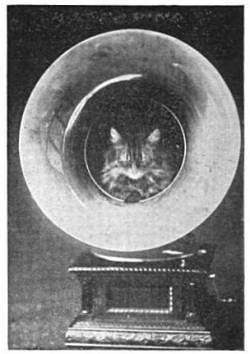
This cat has a liking for the gramophone: it loves to get in the trumpet to sleep, and will not move even when a record is put in and played!
— Strand, August 1906