Search Results for: lee sallows
A Dudeney Square
From Lee Sallows:
“In his book Amusements in Mathematics, H.E. Dudeney presents a method of classifying 4×4 magic squares based on the distribution of their 8 complementary pairs 1 & 16, 2 & 15, .., 8 & 9. There are just 12 distinct such distributions or ‘graphic types’, which he labelled I to XII. The square above is an example of a type X square.”
(Thanks, Lee.)
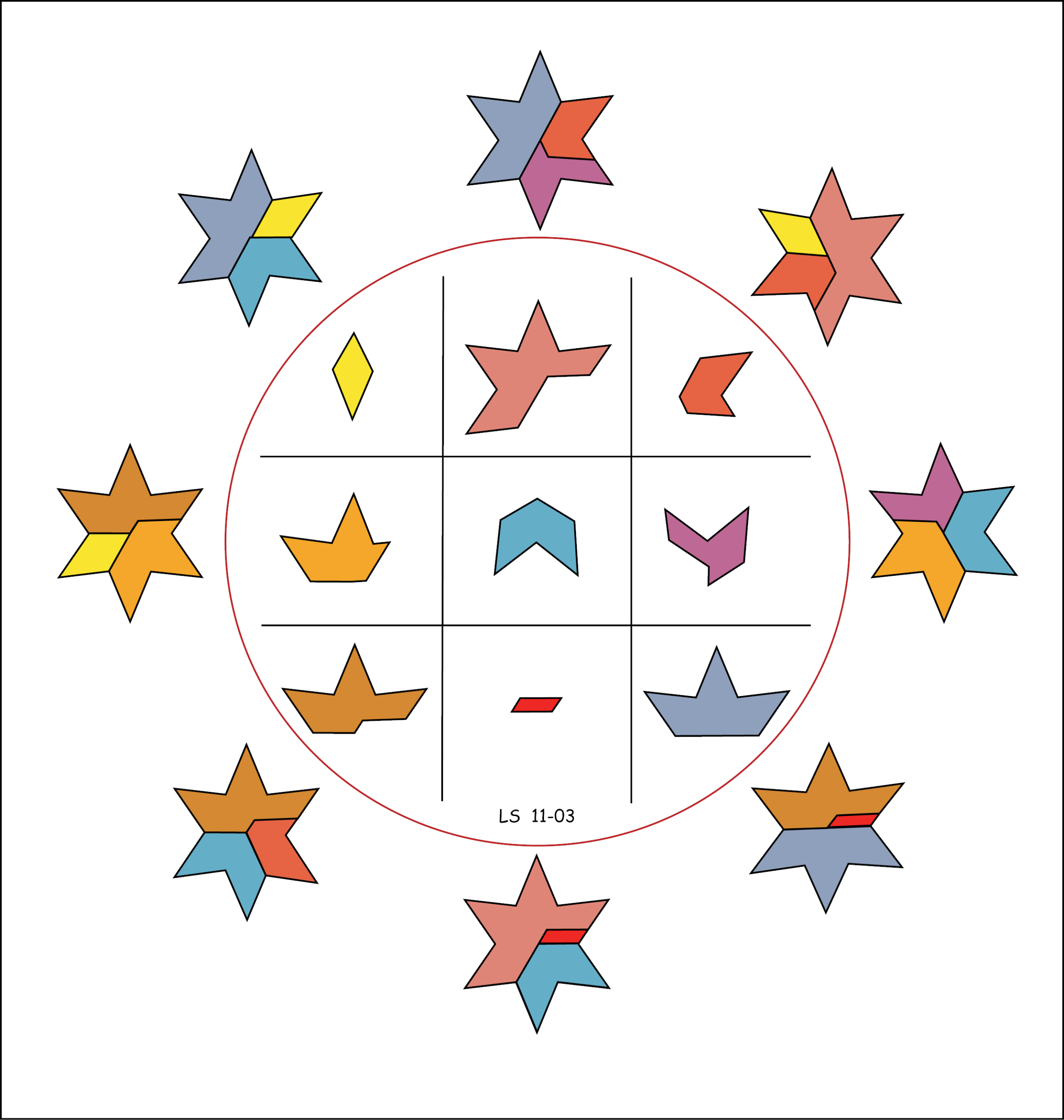
Stellate Thaumaturgy
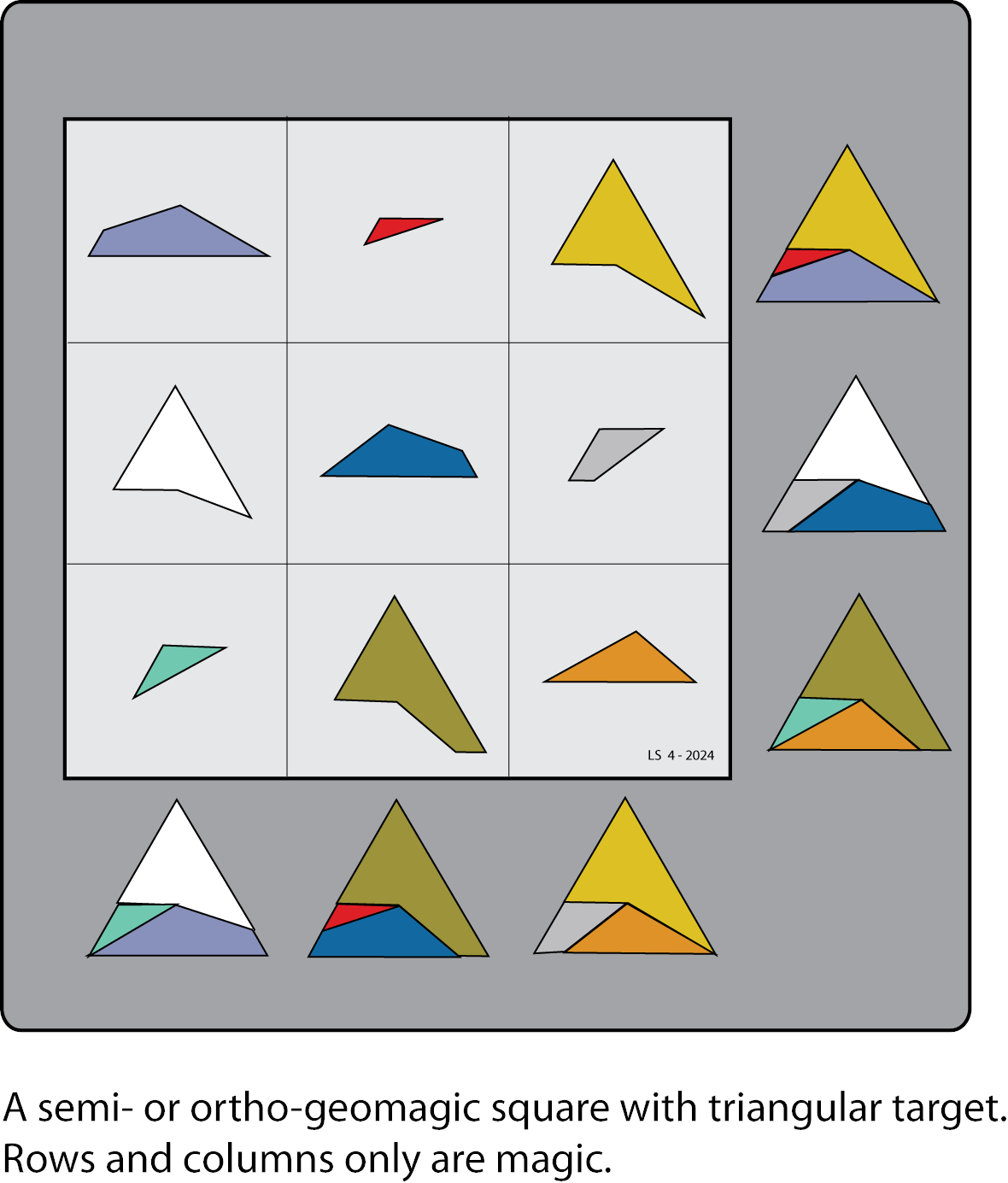
Geomagic
A Self-Intersecting Reflexicon
A Perpetual Motion Device
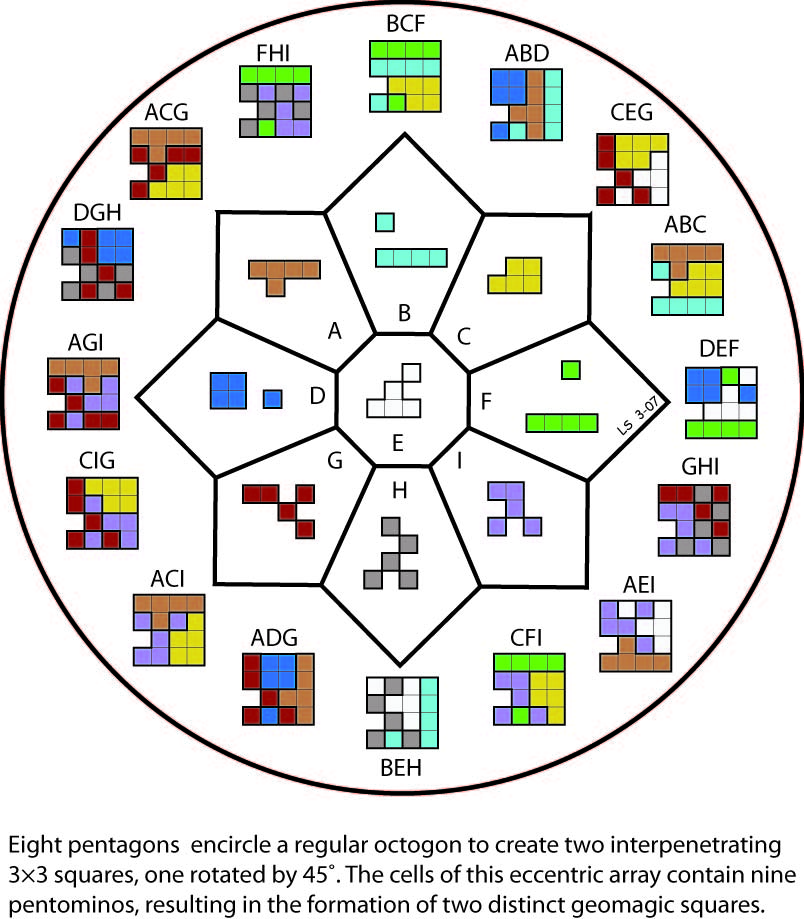
A 3×3 Panmagic Square
From Lee Sallows:
Numerical panmagic squares of 3×3 being impossible, the above square is in fact the first known order-3 panmagic square, a boast it can enjoy until the day that someone comes up with an improved solution. Such as one using all nine connected pieces, say.
Or not, perhaps? For the square above has a further property that other panmagic squares may not possess. Choose any three of the four corner pieces. There are four possibilities: aci, cig, agi and acg. Whatever your choice, the three pieces selected will tile the target.
(Thanks, Lee!)