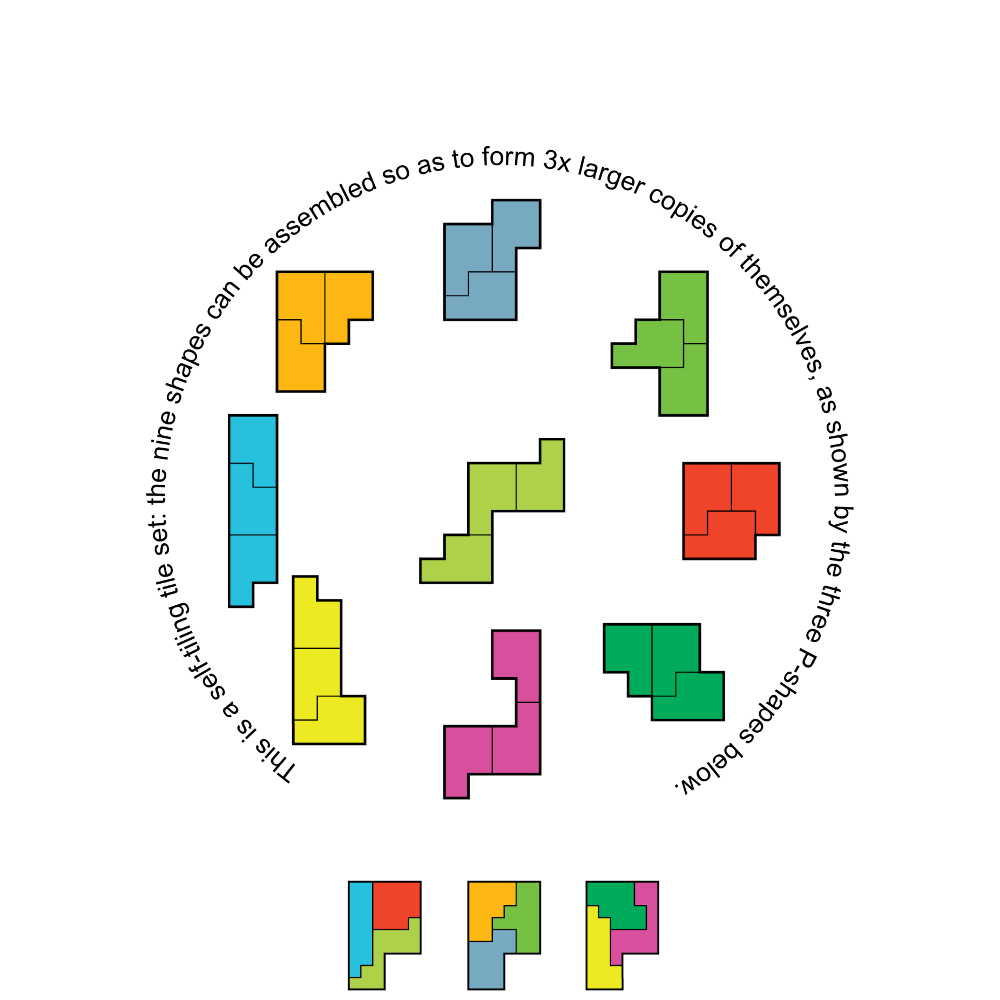Search Results for: lee sallows
Constitutional Crisis
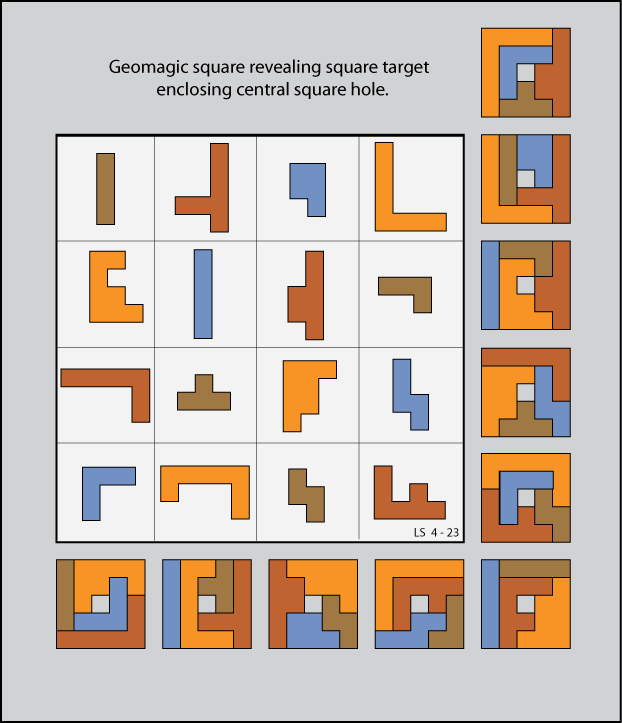
Fair and Square
From Lee Sallows:
(Thanks, Lee!)
Eight Flights
From Lee Sallows, a geomagic square with a staircase theme:
(Thanks, Lee!)
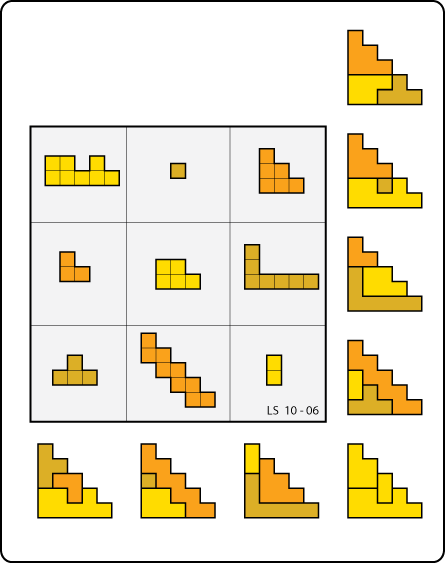
Three by Three
From Lee Sallows:
(Thanks, Lee!)
Chronological Order
By Lee Sallows: If the letters BJFGSDNRMLATPHOCIYVEU are assigned to the integers -10 to 10, then:
J+A+N+U+A+R+Y = -9+0-4+10+0-3+7 = 1 F+E+B+R+U+A+R+Y = -8+9-10-3+10+0-3+7 = 2 M+A+R+C+H = -2+0-3+5+3 = 3 A+P+R+I+L = 0+2-3+6-1 = 4 M+A+Y = -2+0+7 = 5 J+U+N+E = -9+10-4+9 = 6 J+U+L+Y = -9+10-1+7 = 7 A+U+G+U+S+T = 0+10-7+10-6+1 = 8 S+E+P+T+E+M+B+E+R = -6+9+2+1+9-2-10+9-3 = 9 O+C+T+O+B+ER = 4+5+1+4-10+9-3 = 10 N+O+V+E+M+B+E+R = -4+4+8+9-2-10+9-3 = 11 D+E+C+E+M+B+E+R = -5+9+5+9-2-10+9-3 = 12
Similarly, if -7 to 7 are assigned SROEMUNFIDYHTAW, then SUNDAY to SATURDAY take on ordinal values. See Alignment.
(David Morice, “Kickshaws,” Word Ways 24:2 [May 1991], 105-116.)
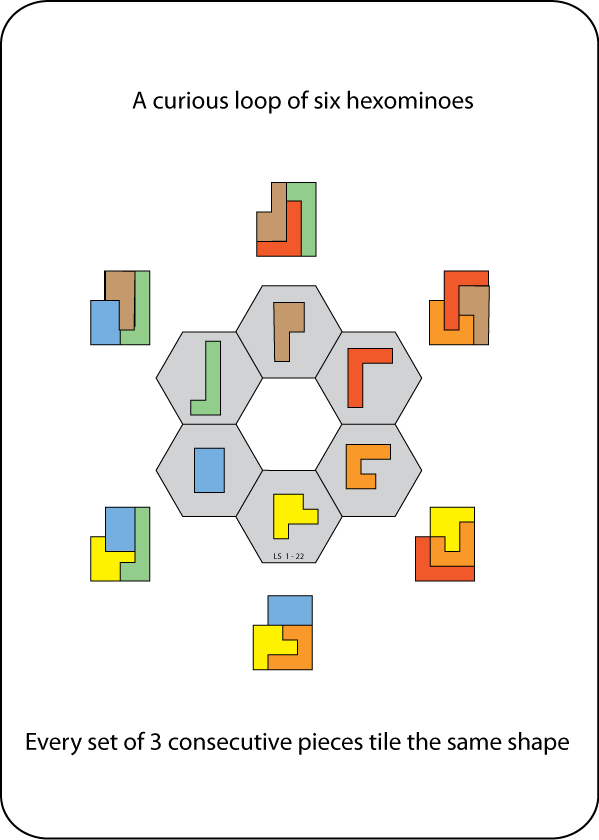
A Self-Tiling Tile Set
A Self-Descriptive Crossword Puzzle
From Lee Sallows:
Can you complete the ‘self-descriptive crossword puzzle’ at left below? As in the solution to a similar puzzle seen at right, each of its 13 entries, 6 horizontal, 7 vertical, consists of an English number name folowed by a space followed by a distinct letter. The number preceding each letter describes the total number of occurrences of the letter in the completed puzzle. Hence, in the example, E occurs thirteen times, G only once, and so on, as readers can check. Note that the self-description is complete; every distinct letter is counted.
Though far from easy, the self-descriptive property of the crossword enables its solution to be inferred from its empty grid using reasoning based on orthography only.
Reciprocation
Another remarkable contribution by Lee Sallows:

(Thanks, Lee!)
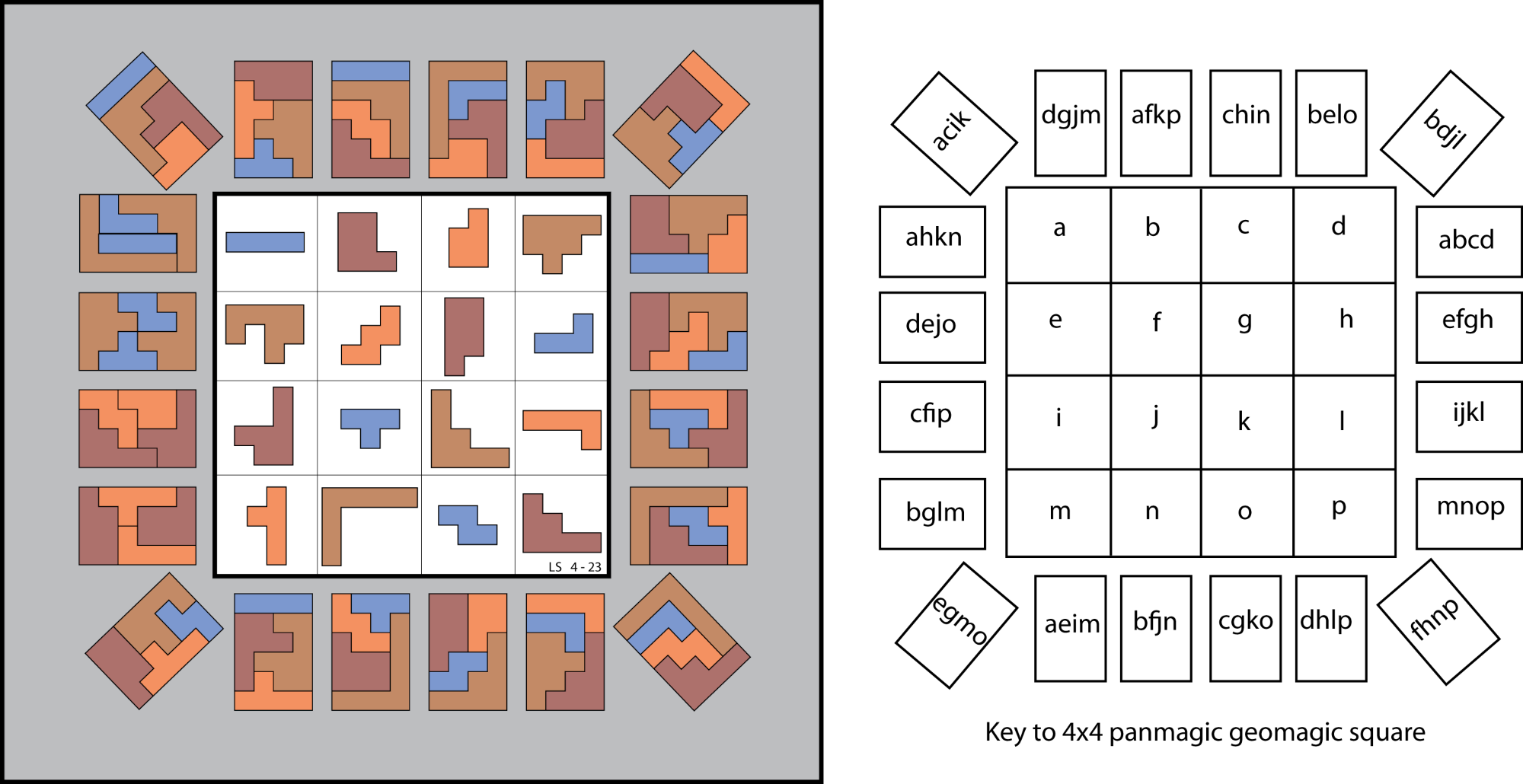
A Panmagic Geomagic Square
Another amazing contribution by Lee Sallows:
“The picture above shows a 4×4 geomagic square, which is to say a magic square using geometrical shapes that can be fitted together so as to form an identical target shape, in this case a 4×6 rectangle, rather than numbers adding to a constant sum. In addition, the square is also panmagic, meaning that besides the usual 4 rows, 4 columns, and both main diagonals, the shapes occupying each of the so-called ‘broken’ diagonals, afkn, dejo, cfip, bglm, chin, belo, are also able to tile the rectangle. Lastly, the 4 shapes contained in the corner cells of the four embedded 3×3 sub-squares, acik, bdjl, fhnp, egmo, are also ‘magic’, bringing the total number of target-tiling shape sets to 20, a small improvement over the 16 achieved by a panmagic-only square. With that said, it is worth noting that 4×4 geomagic squares have been found achieving target-tiling scores as high as 48.”
Click the image to expand it. Thanks, Lee!